RADICALS

To differentiate a function containing a radical, replace the radical by a fractional exponent; then find the derivative by applying the appropriate theorems.

EXAMPLE. Find the derivative of

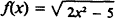
SOLUTION: Replace the radical by the proper fractional exponent, such that

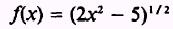
and by Theorem 6

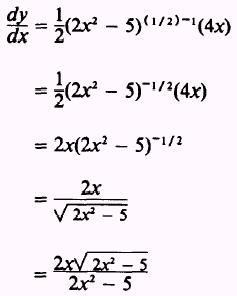
EXAMPLE: Find the derivative of

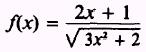
SOL UTION: Replace the radical by the proper fractional exponent, thus

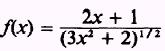
At this point a decision is in order. This problem may be solved by either writing

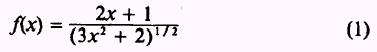
and applying Theorem 6 in the denominator and then applying Theorem 5 for the quotient or writing

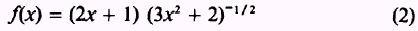
and applying Theorem 6 for the second factor and then applying Theorem 4 for the product.

The two methods of solution are completed individually as follows:

Use equation (1):

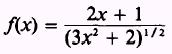
Find the derivative of the denominator

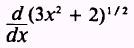
by applying the power theorem

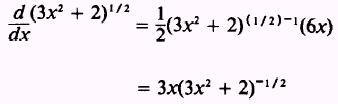
The derivative of the numerator is

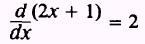
Now apply Theorem 5:

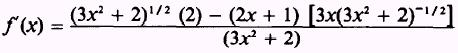
Multiply both numerator and denominator by

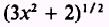
and simplify:

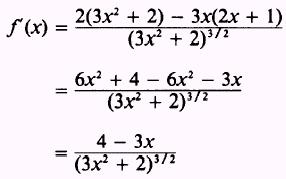
To find the same solution by a different method, use equation (2):

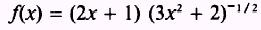
Find the derivative of each factor:

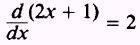
and

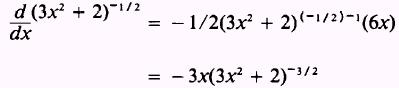
Now apply Theorem 4:

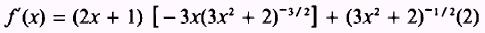
Multiply both numerator and denominator by

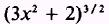
such that,

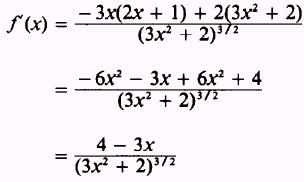
which agrees with the solution of the first method used.

PRACTICE PROBLEMS:

Find the derivatives of the following:

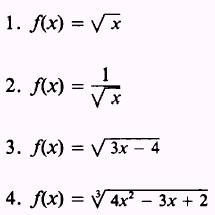
ANSWERS:
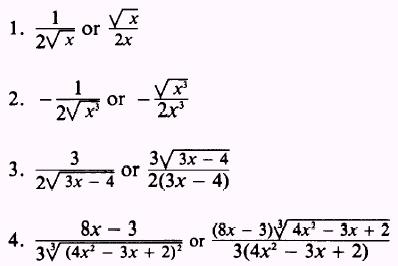