|
PRODUCTS
Theorem 4. The derivative of the product of two differentiable
functions of x is equal to the first function multiplied by the derivative of
the second function, plus the second function multiplied by the derivative of
the first function.
If
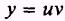
then
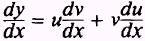
This theorem may be extended to include the product of
three differentiable functions or more. The result for three functions would be
as follows:
if
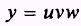
then
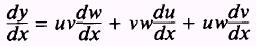
EXAMPLE. Find the derivative of
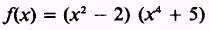
SOLUTION. The derivative of the first factor is 2x, and
the derivative of the second factor is 4x3. Therefore,
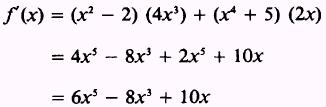
EXAMPLE. Find the derivative of
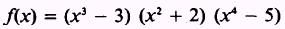
SOLUTION. The derivatives of the three factors, in the
order given, are 3x2, 2x, and 4x3.
Therefore,
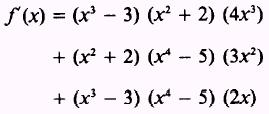
Expanding,
we get
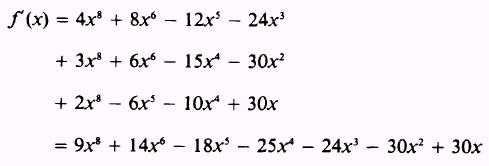
PRACTICE
PROBLEMS:
Find
the derivatives of the following:
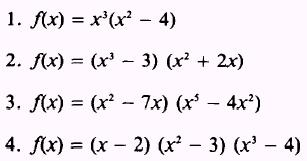
ANSWERS:
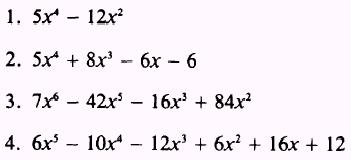
|

