CHAPTER 5 DERIVATIVES

LEARNING OBJECTIVES

Upon completion of this chapter, you should be able to do the following:

1. Compute the derivative of a constant.

2. Compute the derivative of a variable raised to a power.

3. Compute the derivative of the sum and product of two or more functions and the quotient of two functions.

4. Compute the derivative of a function raised to a power, in radical form, and by using the chain rule.

5. Compute the derivative of an inverse function, an implicit function, a trigonometric function, and a natural logarithmic function.

6. Compute the derivative of a constant raised to a variable power.

INTRODUCTION

In the previous chapter on limits, we used the delta process to find the limit of a function as Ax approached zero. We called the result of this tedious and, in some cases, lengthy process the derivative. In this chapter we will examine some rules used to find the derivative of a function without using the delta process. To find how y changes as x changes, we take the limit of

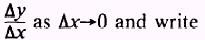
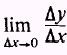
which is called the derivative of y with respect to x; we use the symbol 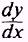to indicate the derivative and write

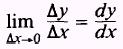
In this section we will learn a number of rules that will enable us to easily obtain the derivative of many algebraic functions. In the derivation of these rules, which will be called theorems, we will assume that

or

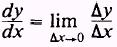
exists and is finite.

DERIVATIVE OF A CONSTANT

The method we will use to find the derivative of a constant is similar to the delta process used in the previous chapter but includes an analytical proof. A diagram is used to give a geometrical meaning of the function.

Theorem 1. The derivative of a constant is zero. Expressed as a formula, this may be written as

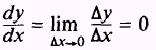
where y = c.

PROOF: In figure 5-1, the graph of

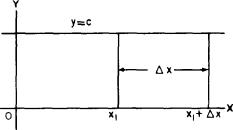
Figure 5-1.-Graph of y = c, where c is a constant.

y=c

where c is a constant, the value of y is the same for all values of x, and any change in x (that is, x) does not affect y; then

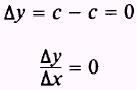
and

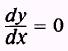
Another way of stating this is that when x is equal to x₁ and when x is equal to 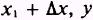has the same value. Therefore,

y=c

and

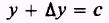
so that

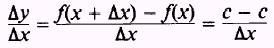
and

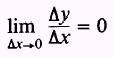
Then

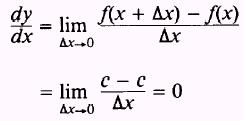
The equation

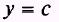
represents a straight line parallel to the X axis. The slope of this line will be zero for all values of x. Therefore, the derivative is zero for all values of x.

EXAMPLE. Find the derivative 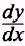of the function

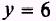
SOLUTION:

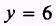
and

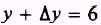
Therefore,
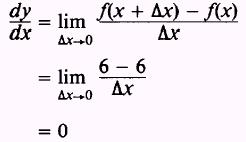