IMPLICIT FUNCTIONS

In equations containing x and y, separating the variables is not always easy. If we do not solve an equation for y, we call y an implicit function of x. In the equation

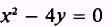
y is an implicit function of x, and x is also called an implicit function of y. If we solve this equation for y, that is

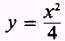
then y would be called an explicit function of x. In many cases such a solution would be far too complicated to handle conveniently.

When y is given by an equation such as

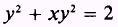
y is an implicit function of x.

Whenever we have an equation of this type in which y is an implicit function of x, we can differentiate the function in a straightforward manner. The derivative of each term containing y will be followed by 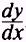. Refer to Theorem 6.

EXAMPLE. Obtain the derivative 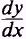of

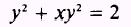
SOL UTI0Y- Find the derivative of y²:

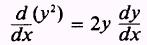
the derivative of xy²:

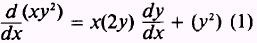
and the derivative of 2:

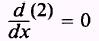
such that,

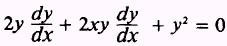
Solving for 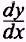we find that

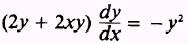
and

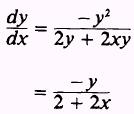
Thus, whenever we differentiate an implicit function, the derivative will usually contain terms in both x and y.

PRACTICE PROBLEMS:

Find the derivative 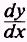of the following:

ANSWERS:
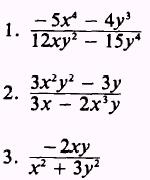