The equations of the asymptotes were given earlier as

bx+ay=0 and bx-ay=0

or

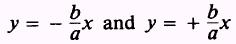
The earlier reference also pointed out that the length of the focal chord is equal to .

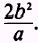Note that you have no restriction of a > b for the hyperbola as you have for the ellipse. Instead, the direction in which the hyperbola opens corresponds to the transverse axis on which the foci and vertices lie.

The properties of a hyperbola can be determined from the equation of a hyperbola or the equation can be written given certain properties, as shown in the following examples. In these examples and in the practice problems immediately following, all of the hyperbolas considered have their centers at the origin.

EXAMPLE: Find the equation of the hyperbola with an eccentricity of 3/2, directrices x = 4/3, and foci at ( 3,0).

SOLUTION: The foci lie on the X axis at the points (3,0) and ( - 3,0), so the equation is of the form

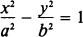
This fact is also shown by the equation of the directrices.

Since we have determined the form of the equation and since the center of the curve in this section is restricted to the origin, the problem is reduced to finding the values of a² and b².

First, the foci are given as ( 3,0); and since the foci are also the points ( c,0), then

c=3

The eccentricity is given and the value of a² can be determined from the formula

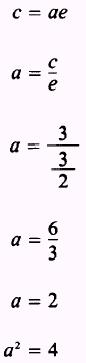
The relationship of a, b, and c for the hyperbola is

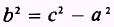
and

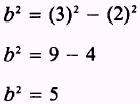
When these values are substituted in the equation

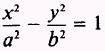
the equation

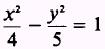
results and is the equation of the hyperbola.

The equation could also be found by the use of other relationships using the given information.

The directrices are given as

and, since

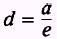
or

a=de

substituting the values given for d and e results in

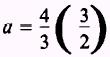
therefore,

a=2

and

a² = 4

While the value of c can be determined by the given information in this problem, it could also be computed since

c = ae

and a has been found to equal 2 and e is given as 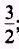; therefore,

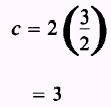
With values for a and c computed, the value of b is found as before and the equation can be written.

EXAMPLE: Find the foci, directrices, eccentricity, length of the focal chord, and equations of the asymptotes of the hyperbola described by the equation

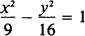
SOLUTION: This equation is of the form

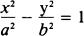
and the values for a and b are determined by inspection to be

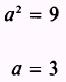
and

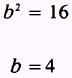
With a and b known, we find c by using the formula

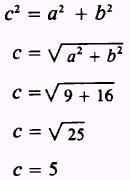
From the form of the equation, we know that the foci are at the points

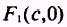
and

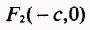
so the foci =

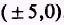
The eccentricity is found by the formula

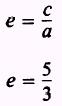
Figure 2-17 shows that with the center at the origin, c and a will have the same sign.

The directrix is found by the formula

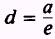
or, since this equation will have directrices parallel to the Y axis, by the formula

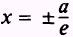
Then

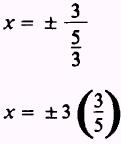
So the directrices are the lines

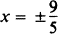
The focal chord (f .c.) is found by

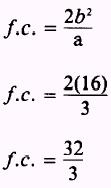
Finally, the equations of the asymptotes are the equations of the two straight lines:

bx+ay=0

and

bx-ay=0

In this problem, substituting the values of a and b in each equation gives

4x+3y=0

and

4x-3y=0

or

4x3y=0

The equations of the lines asymptotic to the curve can also be written in the form

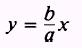
and

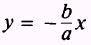
In this form the lines are

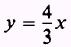
and

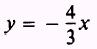
or

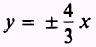
If we think of this equation as a form of the slope-intercept formula

y=mx+b

from chapter 1, the lines would have slopes of 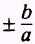and each would have its y intercept at the origin as shown in figure 2-18.