MULTIPLE-LOAD VOLTAGE DIVIDERS
A multiple-load voltage divider is shown in figure 3-65. An important point that was not emphasized before is that when using the 10% rule-of-thumb to calculate the bleeder current, you must take 10% of the total load current.

Figure 3-65. - Multiple-load voltage divider.

Given the information shown in figure 3-65, you can calculate the values for the resistors needed in the voltage-divider circuits. The same steps will be followed as in the previous voltage divider problem.

Given:



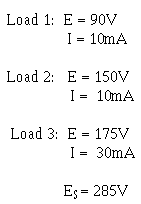
The bleeder current should be 10% of the total load current.

Solution:


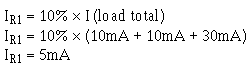
Since the voltage across R₁ (E_R1) is equal to the voltage requirement for load 1, Ohm's law can be used to calculate the value for R₁.

Solution:


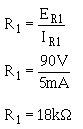
The current through R₂ (I_R2) is equal to the current through R₁plus the current through load 1.

Solution:


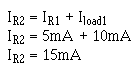
The voltage across R₂ (E_R2) is equal to the difference between the voltage requirements of load 1 and load 2.


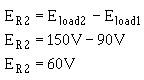
Ohm's law can now be used to solve for the value of R₂.

Solution:


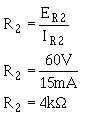
The current through R₃ (I_R3) is equal to the current through R₂ plus the current through load 2.


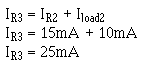
The voltage across R₃ (E_R3) equals the difference between the voltage requirement of load 3 and load 2.


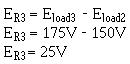
Ohm's law can now be used to solve for the value of R ₃.

Solution:


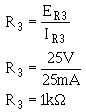
The current through R₄ (I_R4) is equal to the current through R₃ plus the current through load 3. I_R4 is equal to total circuit current (I _T).


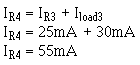
The voltage across R₄ (E_R4) equals the difference between the source voltage and the voltage requirement of load 3.


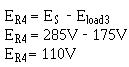
Ohm's law can now be used to solve for the value of R ₄.

Solution:


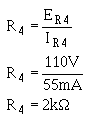
With the calculations just explained, the values of the resistors used in the voltage divider are as follows:
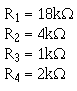