KIRCHHOFF'S VOLTAGE LAW

In 1847, G. R. Kirchhoff extended the use of Ohm's law by developing a simple concept concerning the voltages contained in a series circuit loop. Kirchhoff's voltage law states:

"The algebraic sum of the voltage drops in any closed path in a circuit and the electromotive forces in that path is equal to zero."

To state Kirchhoff's law another way, the voltage drops and voltage sources in a circuit are equal at any given moment in time. If the voltage sources are assumed to have one sign (positive or negative) at that instant and the voltage drops are assumed to have the opposite sign, the result of adding the voltage sources and voltage drops will be zero.

NOTE: The terms electromotive force and emf are used when explaining Kirchhoff's law because Kirchhoff's law is used in alternating current circuits (covered in Module 2). In applying Kirchhoff's law to direct current circuits, the terms electromotive force and emf apply to voltage sources such as batteries or power supplies.

Through the use of Kirchhoff's law, circuit problems can be solved which would be difficult, and often impossible, with knowledge of Ohm's law alone. When Kirchhoff's law is properly applied, an equation can be set up for a closed loop and the unknown circuit values can be calculated.

POLARITY OF VOLTAGE
To apply Kirchhoff's voltage law, the meaning of voltage polarity must be understood.

In the circuit shown in figure 3-22, the current is shown flowing in a counterclockwise direction. Notice that the end of resistor R₁, into which the current flows, is marked NEGATIVE (-). The end of R₁ at which the current leaves is marked POSITIVE (+). These polarity markings are used to show that the end of R₁ into which the current flows is at a higher negative potential than the end of the resistor at which the current leaves. Point A is more negative than point B.

Figure 3-22. - Voltage polarities.

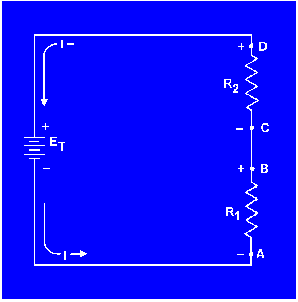
Point C, which is at the same potential as point B, is labeled negative. This is to indicate that point C is more negative than point D. To say a point is positive (or negative) without stating what the polarity is based upon has no meaning. In working with Kirchhoff's law, positive and negative polarities are assigned in the direction of current flow.