|
Rules for Parallel DC Circuits
The same voltage exists across each branch of a parallel
circuit and is equal to the source voltage.
The current through a branch of a parallel network is inversely proportional to the amount of resistance of the branch.
The total current of a parallel circuit is equal to the sum of the individual branch currents of the circuit.
The total resistance of a parallel circuit is found by the general formula:

or one of the formulas derived from this general formula.
The total power consumed in a parallel circuit is equal to the sum of the power consumptions of the individual resistances.
SOLVING PARALLEL CIRCUIT PROBLEMS
Problems involving the determination of resistance, voltage, current, and power in a parallel circuit are solved as simply as in a series circuit. The procedure is the same - (1) draw the circuit diagram, (2) state the values given and the values to be found, (3) select the equations to be used in solving for the unknown quantities based upon the known quantities, and (4) substitute the known values in the equation you have selected and solve for the unknown value.
Example: A parallel circuit consists of five resistors. The value of each resistor is known and the current through R1 is known. You are asked to calculate the value for total resistance, total power, total current, source voltage, the power used by each resistor, and the current through resistors R2, R3,R4, and R5.
Given:

Find:

This may appear to be a large amount of mathematical manipulation. However, if you use the step-by-step approach, the circuit will fall apart quite easily.
The first step in solving this problem is for you to draw the circuit and indicate the known values as shown in figure 3-50.
Figure 3-50. - Parallel circuit problem.

There are several ways to approach this problem. With the values you have been given, you could first solve for RT, the power used by R1, or the voltage across R1 , which you know is equal to the source voltage and the voltage across each of the other resistors. Solving for RT or the power used by R1 will not help in solving for the other unknown values.
Once the voltage across Rl is known, this value will help you calculate other unknowns. Therefore the logical unknown to solve for is the source voltage (the voltage across R1).
Given:

Solution:

Now that source voltage is known, you can solve for current in each branch.
Given:

Solution:

Since R3 = R4 = R5 and the voltage across each branch is the same:

Solving for total resistance.
Given:
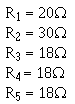
Solution:

An alternate method for solving for RT can be used. By observation, you can see that R3, R 4, and R5 are of equal ohmic value. Therefore an equivalent resistor can be substituted for these three resistors in solving for total resistance.
Given:

Solution:

The circuit can now be redrawn using a resistor labeled Req1 in place of R3, R4, and R5 as shown in figure 3-51.
Figure 3-51. - First equivalent parallel circuit.

An equivalent resistor can be calculated and substituted for R l and R2 by use of the product over the sum formula.
Given:

Solution:

The circuit is now redrawn again using a resistor labeled Req2 in place of R1 and R2 as shown in figure 3-52.
Figure 3-52. - Second equivalent parallel circuit.

You are now left with two resistors in parallel. The product over the sum method can now be used to solve for total resistance.
Given:

Solution:

This agrees with the solution found by using the general formula for solving for resistors in parallel.
The circuit can now be redrawn as shown in figure 3-53 and total current can be calculated.
Figure 3-53. - Parallel circuit redrawn to final equivalent circuit.

Given:

Solution:

This solution can be checked by using the values already calculated for the branch currents.
Given:

Solution:

Now that total current is known, the next logical step is to find total power.
Given:

Solution:

Solving for the power in each branch.
Given:

Solution:

Since IR3 = IR4 = IR5 then, PR3 = PR4 = PR5 = 1800 W. The previous calculation for total power can now be checked.
Given:

Solution:

What term identifies a single resistor that represents total resistance of a complex circuit?
The total power in both series and parallel circuits is computed with the formula: PT = P1 + P2 + P3
+...Pn. Why can this formula be used for both series and parallel circuits?
A circuit consists of three resistors connected in parallel across a voltage source. Rl = 40Ω, R 2 = 30Ω, R3 = 40Ω, and P R3 = 360 watts. Solve for RT, E s and IR2. (Hint: Draw and label the circuit first.)
|
|



