Resistance in a Parallel Circuit
In the example diagram, figure 3-44, there are two resistors connected in parallel across a 5-volt battery. Each has a resistance value of 10 ohms. A complete circuit consisting of two parallel paths is formed and current flows as shown.

Figure 3-44. - Two equal resistors connected in parallel.

Computing the individual currents shows that there is one-half of an ampere of current through each resistance. The total current flowing from the battery to the junction of the resistors, and returning from the resistors to the battery, is equal to 1 ampere.

The total resistance of the circuit can be calculated by using
the values of total voltage (E_T) and total current (I_T).

NOTE: From this point on the abbreviations and symbology for electrical quantities will be used in example problems.

Given:


Solution:


This computation shows the total resistance to be 5 ohms; one-half the value of either of the two resistors.

Since the total resistance of a parallel circuit is smaller than any of the individual resistors, total resistance of a parallel circuit is not the sum of the individual resistor values as was the case in a series circuit. The total resistance of resistors in parallelis also referred to as EQUIVALENT RESISTANCE (R_eq). The terms total resistance and equivalent resistance are used interchangeably.

There are several methods used to determine the equivalent resistance of parallel circuits. The best method for a given circuit depends on the number and value of the resistors. For the circuit described above, where all resistors have the same value, the following simple equation is used:


This equation is valid for any number of parallel resistors of EQUAL VALUE.

Example. Four 40-ohm resistors are connected in parallel. What is their equivalent resistance?

Given:


Solution:


Figure 3-45 shows two resistors of unequal value in parallel. Since the total current is shown, the equivalent resistance can be calculated.

Figure 3-45. - Example circuit with unequal parallel resistors.


Given:


Solution:


The equivalent resistance of the circuit shown in figure 3-45 is smaller than either of the two resistors (R ₁, R₂). An important point to remember is that the equivalent resistance of a parallel circuit is always less than the resistance of any branch.

Equivalent resistance can be found if you know the individual resistance values and the source voltage. By calculating each branch current, adding the branch currents to calculate total current, and dividing the source voltage by the total current, the total can be found. This method, while effective, is somewhat lengthy. A quicker method of finding equivalent resistance is to use the general formula for resistors in parallel:


If you apply the general formula to the circuit shown in figure 3-45 you will get the same value for equivalent resistance (2Ω) as was obtained in the previous calculation that used source voltage and total current.

Given:


Solution:


Convert the fractions to a common denominator.


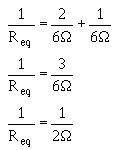
Since both sides are reciprocals (divided into one), disregard the reciprocal function.


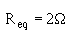
The formula you were given for equal resistors in parallel


is a simplification of the general formula for resistors in parallel


There are other simplifications of the general formula for resistors in parallel which can be used to calculate the total or equivalent resistance in a parallel circuit.

RECIPROCAL METHOD. - This method is based upon taking the reciprocal of each side of the equation. This presents the general formula for resistors in parallel as:


This formula is used to solve for the equivalent resistance of a number of unequal parallel resistors. You must find the lowest common denominator in solving these problems. If you are a little hazy on finding the lowest common denominator, brush up on it in Mathematics Volume 1, NAVEDTRA 10069 (Series).

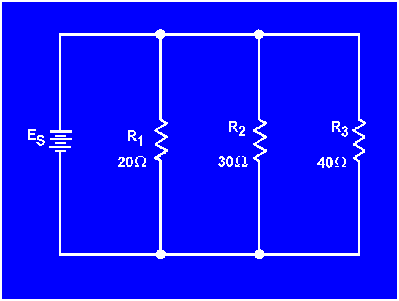
Example: Three resistors are connected in parallel as shown in figure 3-46. The resistor values are: R₁ = 20 ohms, R₂ = 30 ohms, R₃ = 40 ohms. What is the equivalent resistance? (Use the reciprocal method.)

Figure 3-46. - Example parallel circuit with unequal branch resistors.


Given:


Solution:



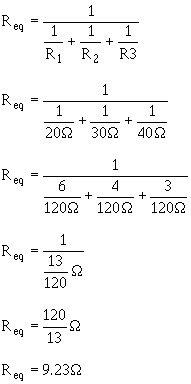
PRODUCT OVER THE SUM METHOD. - A convenient method for finding the equivalent, or total, resistance of two parallel resistors is by using the following formula.


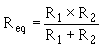
This equation, called the product over the sum formula, is used so frequently it should be committed to memory.

Example. What is the equivalent resistance of a 20-ohm and a 30-ohm resistor connected in parallel, as in figure 3-47?

Figure 3-47. - Parallel circuit with two unequal resistors.

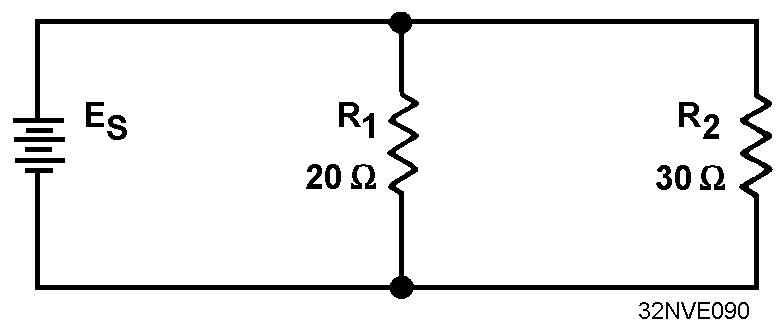
Given:


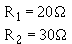
Solution:


Four equal resistors are connected in parallel, each resistor has an ohmic value of 100 ohms, what is the equivalent resistance?

Three resistors connected in parallel have values of 12 kΩ, 20 kΩ, and 30 kΩ. What is the equivalent resistance?

Two resistors connected in parallel have values of 10 kΩ and 30 kΩ. What is the equivalent resistance?