Voltage in a Series Circuit

The voltage dropped across the resistor in a circuit consisting of a single resistor and a voltage source is the total voltage across the circuit and is equal to the applied voltage. The total voltage across a series circuit that consists of more than one resistor is also equal to the applied voltage, but consists of the sum of the individual resistor voltage drops. In any series circuit, the SUM of the resistor voltage drops must equal the source voltage. This statement can be proven by an examination of the circuit shown in figure 3-17. In this circuit a source potential (E_T) of 20 volts is dropped across a series circuit consisting of two 5-ohm resistors. The total resistance of the circuit (R_T ) is equal to the sum of the two individual resistances, or 10 ohms. Using Ohm's law the circuit current may be calculated as follows:



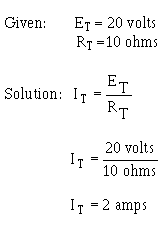
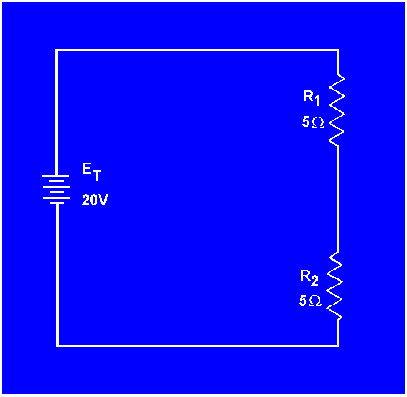
Figure 3-17. - Calculating individual voltage drops in a series circuit.

Since the value of the resistors is known to be 5 ohms each, and the current through the resistors is known to be 2 amperes, the voltage drops across the resistors can be calculated. The voltage (E₁) across R₁ is therefore:


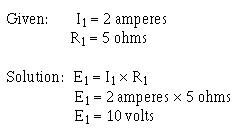
By inspecting the circuit, you can see that R₂ is the same ohmic value as R₁ and carries the same current. The voltage drop across R₂ is therefore also equal to 10 volts. Adding these two 10-volts drops together gives a total drop of 20 volts, exactly equal to the applied voltage. For a series circuit then:

E_T = E₁ = E₂ + E₃ = . . . E_n

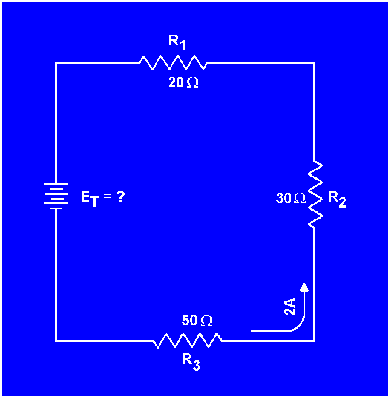
Example: A series circuit consists of three resistors having values of 20 ohms, 30 ohms, and 50 ohms, respectively. Find the applied voltage if the current through the 30 ohm resistor is 2 amps. (The abbreviation amp is commonly used for ampere.)

To solve the problem, a circuit diagram is first drawn and labeled (fig 3-18).

Figure 3-18. - Solving for applied voltage in a series circuit.




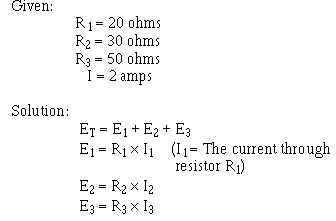
Substituting:


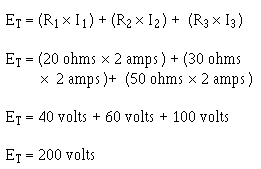
NOTE: When you use Ohm's law, the quantities for the equation MUST be taken from the SAME part of the circuit. In the above example the voltage across R₂ was computed using the current through R ₂ and the resistance of R₂.

The value of the voltage dropped by a resistor is determined by the applied voltage and is in proportion to the circuit resistances. The voltage drops that occur in a series circuit are in direct proportion to the resistances. This is the result of having the same current flow through each resistor - the larger the ohmic value of the resistor, the larger the voltage drop across it.

A series circuit consisting of three resistors has a current of 3 amps. If R₁ = 20 ohms, R₂=60 ohms, and R₃ = 80 ohms, what is the (a) total resistance and (b) source voltage of the circuit?

What is the voltage dropped by each resistor of the circuit described in question 17?

If the current was increased to 4 amps, what would be the voltage drop across each resistor in the circuit described in question 17?

What would have to be done to the circuit described in question 17 to increase the current to 4 amps?