SERIES DC CIRCUITS

When two unequal charges are connected by a conductor, a complete pathway for current exists. An electric circuit is a complete conducting pathway. It consists not only of the conductor, but also includes the path through the voltage source. Inside the voltage source current flows from the positive terminal, through the source, emerging at the negative terminal.

SERIES CIRCUIT CHARACTERISTICS

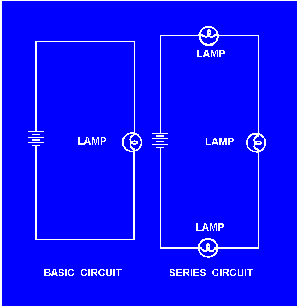
A SERIES CIRCUIT is defined as a circuit that contains only ONE PATH for current flow. To compare the basic circuit that has been discussed and a more complex series circuit, figure 3-13 shows two circuits. The basic circuit has only one lamp and the series circuit has three lamps connected in series.

Figure 3-13. - Comparison of basic and series circuits.


Resistance in a Series Circuit
Referring to figure 3-13, the current in a series circuit must flow through each lamp to complete the electrical path in the circuit. Each additional lamp offers added resistance. In a series circuit, THE TOTAL CIRCUIT RESISTANCE (R_T) IS EQUAL TO THE SUM OF THE INDIVIDUAL RESISTANCES.

As an equation: R_T = R₁ + R₂ + R₃+ . . . R_n

NOTE: The subscript n denotes any number of additional resistances that might be in the equation.

Example: In figure 3-14 a series circuit consisting of three resistors: one of 10 ohms, one of 15 ohms, and one of 30 ohms, is shown. A voltage source provides 110 volts. What is the total resistance?

Figure 3-14. - Solving for total resistance in a series circuit.





In some circuit applications, the total resistance is known and the value of one of the circuit resistors has to be determined. The equation R_T = R₁ + R₂ + R₃ can be transposed to solve for the value of the unknown resistance.

Example: In figure 3-15 the total resistance
of a circuit containing three resistors is 40 ohms. Two of the circuit resistors are 10 ohms each. Calculate the value of the third resistor (R₃ ).

Figure 3-15. - Calculating the value of one resistance in a series circuit.