TRIGONOMETRIC FUNCTIONS

Trigonometric functions, which comprise one group of transcendental functions, may be differentiated and integrated in the same fashion as the other functions. We will limit our proofs to the sine, cosine, and secant functions but will list several others.

Formula.

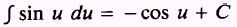
PROOF:

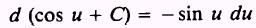
and

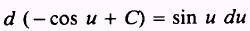
Therefore,

Formula.

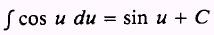
PROOF:

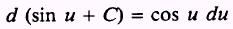
Therefore,

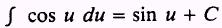
Formula.

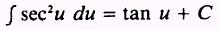
PROOF:

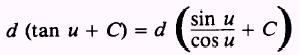
and by the quotient rule

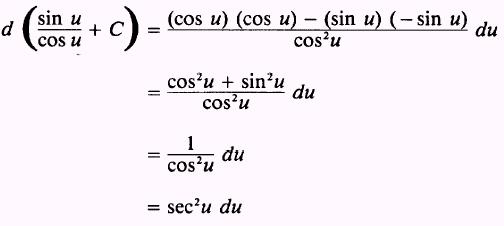
Therefore,

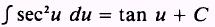
To this point we have considered integrals of trigonometric functions that result in functions of the sine, cosine, and tangent. Those integrals that result in functions of the cotangent, secant, and cosecant are included in the following list of elementary integrals:

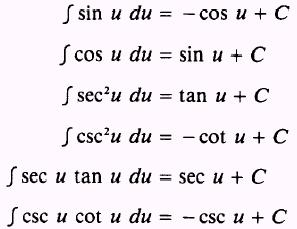
EXAMPLE: Evaluate

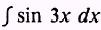
SOLUTION: We need the integral in the form of

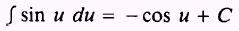
We let

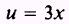
so that

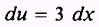
but we do not have 3 dx. Therefore, we multiply the integral by 3/3 and rearrange as follows:

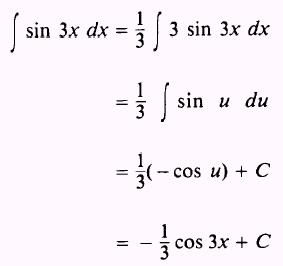
EXAMPLE: Evaluate

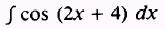
SOLUTION: Let

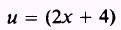
so that

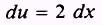
Therefore,

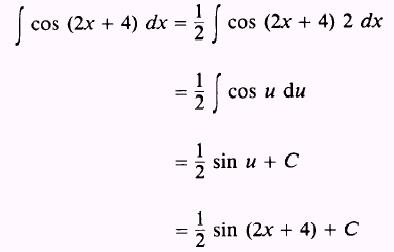
EXAMPLE: Evaluate

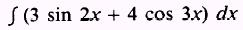
SOLUTION: We use the rule for sums and write

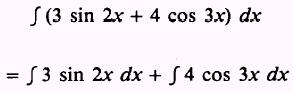
Then, in the integral

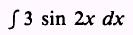
let

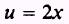
so that

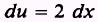
but we have

3 dx

Hence, proper compensation has to be made as follows:

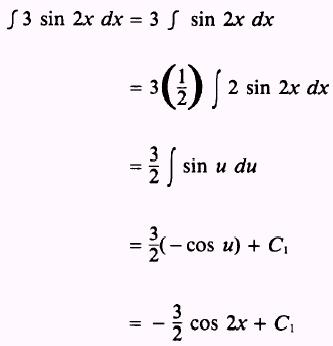
The second integral

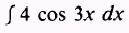
with

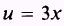
and

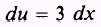
is evaluated as follows:

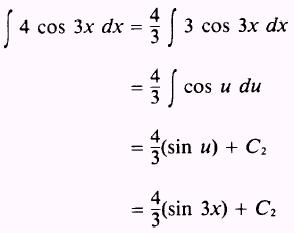
Then, by combining the two solutions, we have

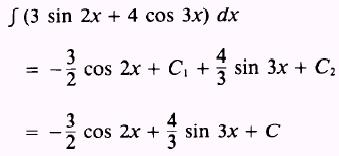
where

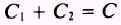
EXAMPLE: Evaluate

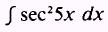
SOL UTION: Let

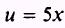
so that

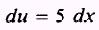
We need 5 dx so we write

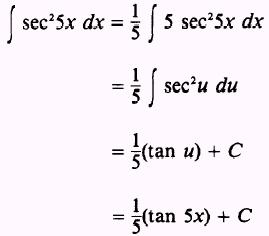
EXAMPLE: Evaluate

SOL UTION: Let

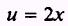
so that

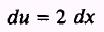
We require du equal to 2 dx, so we write

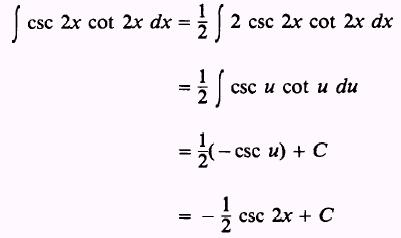
EXAMPLE: Evaluate

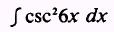
SOL UTION: Let

u=6x

so that

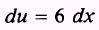
then,

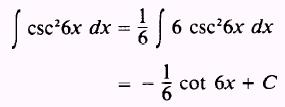
EXAMPLE: Evaluate

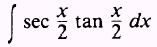
SOL UTION: Let

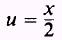
so that

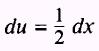
then,
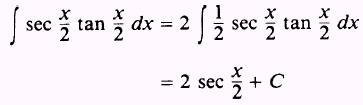