PROOF:

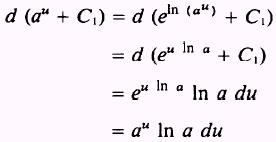
so that

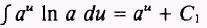
But In a is a constant, so

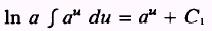
Then, by dividing both sides by In a:

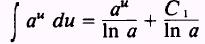
or

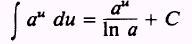
where

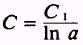
EXAMPLE: Evaluate

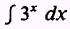
SOLUTION: Let

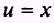
so that

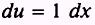
Therefore, by knowing that

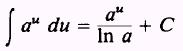
and using substitution, we find that

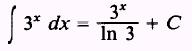
EXAMPLE: Evaluate

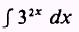
SOLUTION. Let

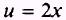
so that

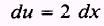
The integral should contain a factor of 2. Thus we insert a factor of 2 in the integral and compensate by multiplying the integral by 1/2.

Then,

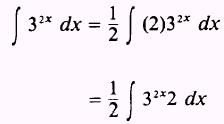
Therefore,

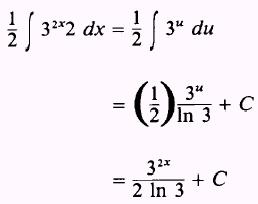
EXAMPLE: Evaluate

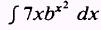
SOLUTION: Let

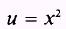
so that

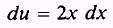
We find we need 2x dx; therefore, we remove the 7 and insert a 2 by writing

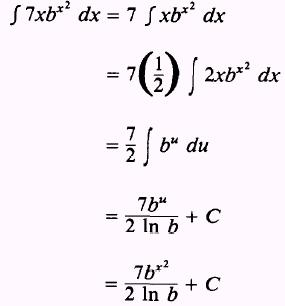
PRACTICE PROBLEMS: Evaluate the following integrals:

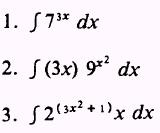
ANSWERS:
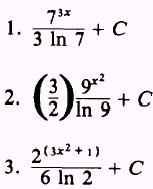