Uneven Division

In some division problems such as 7 3, there is no other whole number that, when multiplied by the divisor, will give the dividend. We use the distributive idea to show how division is done in such a case. For example, 7 3 could be written as follows:

Thus, we see that the quotient also carries one unit that is to be divided by 3. It should now be clear that and that this can be further reduced as follows:

In elementary arithmetic the part of the dividend that cannot be divided evenly by the divisor is often called a REMAINDER and is placed next to the quotient with the prefix R. Thus, in the foregoing example where the quotient was 12 , the quotient could be written 12 R 1. This method of indicating uneven division is useful in examples such as the following:

Suppose that $13 is available for the purchase of spare parts, and the parts needed cost $3 each. Four parts can be bought with the available money, and $1 will be left over. Since it is not possible to buy l/3 of a part, expressing the result as 4 R 1 gives a more meaningful answer than 4 l/3.

Placement of Decimal Points In division, as in multiplication, the placement of the decimal point is important. Determining the location of the decimal point and the number of places in the quotient can be relatively simple if the work is kept in the proper columns. For example, notice the vertical alignment in the following problem:

We notice that the first two places in the dividend are used to obtain the first place in the quotient. Since 3 is in the hundreds column there are two more places in the quotient (tens place and units place). The decimal point in the quotient is understood to be directly above the position of the decimal point in the dividend. In the example shown here, the decimal point is not shown but is understood to be immediately after the second 1.

Checking Accuracy The accuracy of a division of numbers can be checked by multiplying the quotient by the divisor and adding the remainder, if any. The result should equal the dividend. Consider the following example:

DENOMINATE NUMBERS

We have learned that denominate numbers are not difficult to add and subtract, provided that units, tens, hundreds, etc., are retained in their respective columns. Multiplication and division of denominate numbers may also be performed with comparative ease, by using the experience gained in addition and subtraction.

Multiplication

In multiplying denominate numbers by integers, no new ideas are needed. If in the problem 3(5 yd 2 ft 6 in.) we remember that we can multiply each part separately to get the correct product (as in the example, 6(8) = 6(3) + 6(5)),  we can easily find the product, as follows:

Simplifying, this is 17 yd 1 ft 6 in.

When one denominate number is multiplied by another, a question arises concerning the products of the units of measurement. The product of one unit times another of the same kind is one square unit. For example, 1 ft times 1 ft is 1 square foot, abbreviated sq ft; 2 in. times 3 in. is 6 sq in.; etc. If it becomes necessary to multiply such numbers as 2 yd 1 ft times 6 yd 2 ft, the foot units may be converted to fractions of a yard, as follows:

    (2 yd 1 ft)(6 yd 2 ft) = (2 l/3 yd)(6 2/3 yd)

In order to complete the multiplication, a knowledge of fractions is needed. Fractions are discussed in chapter 4 of this training course.

Division

The division of denominate numbers requires division of the highest units first; and if there is a remainder, conversion to the next lower unit, and repeated division until all units have been divided.

In the example (24 gal 1 qt 1 pt) + 5, we perform the following steps: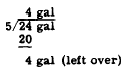

Step 2: Convert the 4 gal left over to 16 qt and add to the 1 qt.

Step 3:

Step 4: Convert the 2 qt left over to 4 pt and add to the 1 pt.

Step 5:

Therefore, 24  gal 1 qt 1 pt. Divided by 5 is 4 gaI. 3 qt 1 pt. 

Practice problem. In problem8 1 through 4, divide as indicated. In problems 5 through 8, multiply or divide as indicated.