The relationships between the angles and the sides of a right triangle are expressed in terms of TRIGONOMETRIC RATIOS. For example, in figure 19-7, the sides of the triangle are named in accordance with their relationship to angle q. In trigonometry, angles are usually named by means of Greek letters. The Greek name of the symbol q is theta.

The six trigonometric ratios for the angle q are listed in table 19-1.

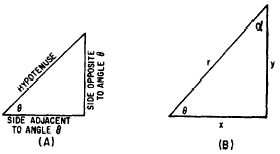
Figure 19-1.-Relationship of sides and angles in a right triangle. (A) Names of the sides; (B) symbols used to designate the sides.

Table 19-1.-Trigonometric ratios.

The other acute angle in figure 19-7 (B) is labeled a (Greek alpha). The side opposite a is x and the side adjacent to a is y. Therefore the six ratios for a are as follows:

Suppose that the sides of triangle (B) in figure 19-7 are as follows: x = 3, y.= 4, r = 5. Then each of the ratios for angles q and a may be expressed as a common fraction or as a decimal. For example,

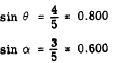
Decimal values have been computed for ratios of angles between 0 and 90, and values for angles above 90" can be expressed in terms of these same values by means of conversion formulas. Appendix II of this training course gives the sine, cosine, and tangent of angles from 0 to 90. The secant, cosecant, and cotangent are calculated, when needed, by using their relationships to the three principal ratios. These relationships are as follows:
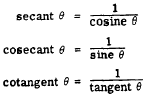