|
SIMILAR RIGHT TRIANGLES
Two right triangles are SIMILAR if one of the
acute angles of the first is equal to one of the
acute angles of the second. This conclusion is
supported by the following reasons:
1. The right angle in the first triangle is equal
to the right angle in the second, since all right
angles are equal.
2. The sum of the angles of any triangle is 180.
Therefore, the sum of the two acute angles in
a right triangle is 90.
3. Let the equal acute angles in the two triangles be represented by A and A
respectively. (See fig. 19-4.) Then the other
acute angles, B and B, are as follows:
B = 90
- A
B = 90
- A
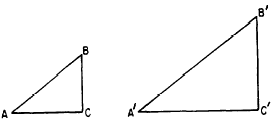
Figure 19-4.-Similar right triangles.
4. Since angles A and A are equal, angles B
and B are also equal.
5. We conclude that two right triangles with one
acute angle of the first equal to one acute angle
of the second have all of their corresponding angles equal. Thus the two
triangles are similar.
Practical situations frequently occur in which
similar right triangles are used to solve problems.
For example, the height of a tree can be determined
by comparing the length of its shadow with
that of a nearby flagpole, as shown in figure
19-5.
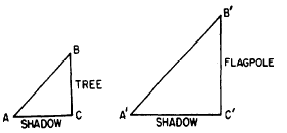
Figure 19-5.-Calculation of height by comparison
of shadows.
Assume that the rays of the sun are parallel and
that the tree and flagpole both form 90 angles
with the ground. Then triangles ABC and ABC
are right triangles and angle B is equal to
angle B . Therefore, the triangles are similar
and their corresponding sides are proportional, with the following result:
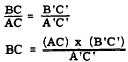
Suppose that the flagpole is known to be 30 feet
high, the shadow of the tree is 12 feet long,
and
the shadow of the flagpole is 24 feet long. Then
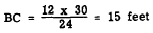
Practice problems.
1. A mast at the top of a building casts a shadow whose
tip is 48 feet from the base of the building. If the building is 12 feet high and
its shadow is 32 feet long,
what is the length of the mast? (NOTE:
If the length of the mast is x, then the height of the
mast above the ground is x + 12.)
2. Figure 19-6 represents an L-shaped building
with dimensions as shown. On the line of sight
from A to D, a stake is driven at C, a point
8 feet from the building and 10 feet from A.
If ABC is a right angle, find the length of AB
and the length of AD. Notice that AE is 18 feet
and ED is 24 feet.
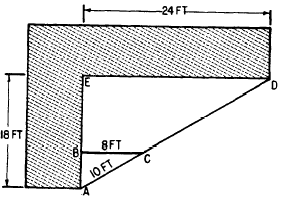
Figure 19-6 - Using similar triangles.
Answers:
1. 6 feet
2. AB = 6 feet
AD = 30 feet
|

