

Custom Search
|
|
  |
|
|
MAXIMUM AND MINIMUM POINTS It will be seen from the graphs of quadratics in one variable that a parabola has a maximum or minimum value, depending on whether the curve opens upward or downward. Thus, when a is negative the curve passes through a maximum value; and when a is positive, the curve passes through a minimum value. Often these maximum or minimum values comprise the only information needed for a particular problem.In higher mathematics it can be shown that the X coordinate, or abscissa, of the maximum or minimum value is
In other words, if we divide minus the coefficient of the x term by twice the coefficient of the x2 term, we have the X coordinate of the maximum or minimum point. If we substitute this value for x in the original equation, the result is the Y value or ordinate, which corresponds to the X value.For example, we know that the graph of the equation x2 + 2x - 8 = y passes through a minimum value because a is positive. To find the coordinates of the point where the parabola has its minimum value, we note that a = 1, b = 2, c = -8. From the rule given above, the X value of the minimum point is
Substituting this value for x in the original equation, we have the value of the Y coordinate of the minimum point. Thus,
The minimum point is (-1, -9). From the graph in figure 16-I (A), we see that these coordinates are correct. Thus, we can quickly and easily find the coordinates of the minimum or maximum point for any quadratic of the form ax2 + bx + c = 0. Practice problems. Without graphing, find the coordinates of the maximum or minimum points for the following equations and state whether they are maximum or minimum.
Answers:
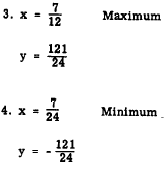
|
|