|
SOLUTION BY FACTORING
The equation x2 - 36 = 0 is a pure quadratic equation,
There are two numbers which, when substituted
for x, will satisfy the equation as follows:
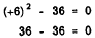
also
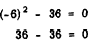
Thus, +6 and - 6 are roots of the equation
x2 - 36 = 0
The most direct way to solve a pure quadratic (one in which no x term appears
and the constant term is a perfect square)
involves rewriting with the constant term in the right member,
as follows:
X2
= 36
Taking square roots on both sides, we have
x = 6
The reason for expressing the solution as both plus
and minus 6 is found in the fact that both +6
and -6, when squared, produce 36.
The equation
x2 - 36 = 0
can also be solved by factoring, as follows:
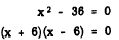
We now have the product of two factors equal to
zero. According to the zero factor law, if a product
is zero, then one or more of its factors is
zero. Therefore, at least one of the factors must
be zero, and it makes no difference which one.
We are free to set first one factor and then
the other factor equal to zero. In so doing we
derive two solutions or roots of the equation. If x + 6 is the factor whose
value is 0, then we have
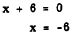
If x - 6 is the zero factor, we have
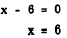
When a three-term quadratic is put into simplest
form, it is customary to place all the terms
on the left side of the equality sign with the
squared term first, the-first-degree term next,
and the constant term last, as in
9x2 - 2x+7=0
If the trinomial in the left member is readily factorable,
the equation can be solved quickly by
separating the trinomial into factors. Consider the equation
3x2 - x - 2 = 0
By factoring the trinomial, the equation becomes
(3x + 2)(x - 1) = 0
Once again we have two factors, the product of which
is 0. This means that one or the other of them
(or both) must have the value 0. If the zero
factor is 3x + 2, we have
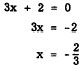
If the zero factor is x - 1, we have
x - 1 = 0
x = 1
Substituting first x = 1 and then x = -2/3 in the
original equation, we see that both roots satisfy
it. Thus,
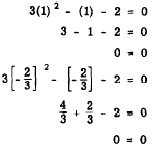
In summation, when a quadratic may be readily
factored, the process for finding its roots
is as follows:.
1. Arrange the equation in the order of the descending
powers of the variable so that all the terms
appear in the left member and zero appears in
the right.
2. Factor the left member of the equation.
3. Set each factor containing the variable equal
to zero and solve the resulting equations.
4. Check by substituting each of the derived roots
in the original equation.
EXAMPLE: Solve the equation x2 - 4x = 12 for
x.
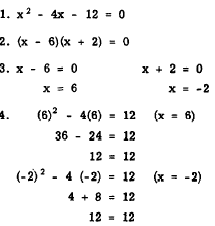
Practice problems. Solve the following equations by factoring:
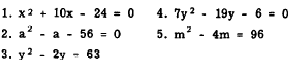
Answers:
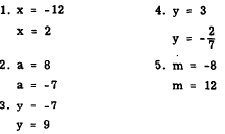
|

