Solution by completing the square

Custom Search

Solution by Factoring

Introduction to Mathematics and Algebra

Solution by the quadratic formula

SOLUTION BY COMPLETING THE SQUARE

When a quadratic cannot be solved by factoring, or the factors are not readily seen, another method of finding the roots is needed. A method that may always be used for quadratics in one variable involves perfect square trinomials. These, we recall, are trinomials whose factors are identical. For example,

x² - 10x + 25 = (x - 5)(x - 5) = (x - 5)²

Recall that in squaring a binomial, the third term of the resulting perfect square trinomial is always the square of the second term of the binomial. The coefficient of the middle term of the trinomial is always twice the second term of the binomial. For example, when (x + 4) is squared, we have

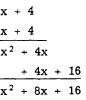
Hence if both the second- and first-degree terms of a perfect square trinomial are known, the third may be written by squaring one-half the coefficient of the first-degree term.

Essentially, in completing the square, certain quantities are added to one member and subtracted from the other, and the equation is so arranged that the left member is a perfect square trinomial. The square roots of both members may then be taken, and the subsequent equalities may be solved for the variable.

For example,

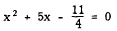
cannot be readily factored. To solve for x by completing the square, we proceed as follows:

1. Leave only the second- and first-degree terms in the left member.

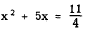
(If the coefficient of x² is not 1, divide through by the coefficient of x².)

2. Complete the square by adding to both members the square of half the coefficient of the x term. In this example, one-half of the coefficient of the x term is 5/2, and the square of 5/2 is 25/4. Thus,

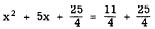
3. Factor the left member and simplify the right member.

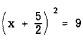
4. Take the square root of both members.

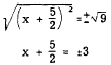
Remember that, in taking square roots on both sides of an equation, we must allow for the fact that two roots exist in every second-degree equation. Thus we designate both the plus and the minus root of 9 in this example.

5. Solve the resulting equations.

6. Check the results.

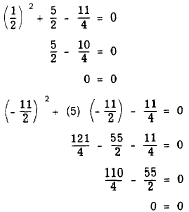
The process of completing the square may always be used to solve a quadratic equation. However, since this process may become complicated in more complex equations, a formula based on completing the square has been developed in which known quantities may be substituted in order to derive the roots of the quadratic equation. This formula is explained in the following paragraphs.