The chain, or civil engineers, scale, commonly referred to as the ENGINEERS SCALE, is usually a triangular scale, containing six fully divided scales that are subdivided decimally, each major interval on a scale being subdivided into 10ths. Figure 2-25 shows the engineers scale and

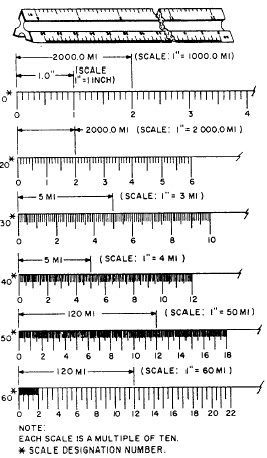
Figure 2-25.-Engineers scale.

segments of each of the six scales. Each of the six scales is designated by a number representing the number of graduations that particular scale has to the linear inch. On the 10 scale, for example, there are 10 graduations to the inch; on the 50 scale there are 50. You can see that the 50 scale has 50 graduations in the same space occupied by 10 on the 10 scale. This space is 1 linear inch.

To determine the actual number of graduations represented by a numeral on the engineers scale, multiply the numeral by 10. On the 50 scale, for instance, the numeral 2 indicates 2 x 10, or 20 graduations from the 0. On the 10 scale, the numeral 11 indicates 11 x 10, or 110 graduations from the 0. Note that the 10 scale is numbered every major graduation, while the 50 scale is numbered every other graduation. Other scales on the engineers scale are the 20, 30, 40, and 60.

Because it is decimally divided, the engineers scale can be used to scale dimensions down to any scale in which the first figure in the ratio is 1 in. and the other is 10, or a multiple of 10. Suppose, for example, that you wanted to scale a dimension of 150 mi down to a scale of 1 in. = 60 mi. You would use the 60 scale, allowing the interval between adjacent graduations to represent 1 mi. To measure off 150 mi to scale on the 60 scale, you would measure off 2.5 in., which falls on the 15th major graduation.

Suppose now that you want to scale a dimension of 6,500 ft down to a scale of 1 in. = 1,000 ft. The second figure in the ratio is a multiple of 10 times a multiple of 10. You would therefore use the 10 scale, allowing the interval between adjacent graduations on the scale to represent 100 ft, in which case the interval between adjacent numerals on the scale would indicate 1,000 ft. To measure off 6,500 ft, you would simply lay off from 0 to 6.5 on the scale.

To use the engineers scale for scaling to scales that are expressed fractionally, you must be able to determine the fractional equivalent of each of the scales. For any scale, this equivalent is simply 1 over the total number of graduations on the scale, or 1 over the product of the scale number times 12, which comes to the same thing. Applying this rule, the fractional expressions of each of the scales is as follows:

Suppose you wanted to scale 50 ft down to a scale of 1/120. The 10 scale gives you this scale; you would therefore use the 10 scale, allowing the space between graduations to represent 1 ft, and measuring off 5 (for 50 ft). The line on your paper would be 5 in. long, representing a line on the object itself that is 120 in. x 5 in., or 600 in., or 50 ft long.

Similarly, if you wanted to scale 50 ft down to a scale of 1/600, you would use the 50 scale and measure off 5 for 50 ft. In this case, the line on your paper would be 1 in. long, representing a line on the object itself that is 1 x 600, or 600 in., or 50 ft long.

When it is not required that the drawing be made to a specified scalethat is, when the dimensions of lines on the drawing are not required to bear a specified ratio to the dimensions of lines on the object itselfthe most convenient scale on the engineers scale is used. Suppose, for example, that you want to draw the outline of a 360-ft by 800-ft rectangular field on an 8-in, by 10 1/2-in. sheet of paper with no specific scale prescribed. All you want to do is reduce the representation of the object to one that will fit the dimensions of the paper. You could use the 10 scale, allowing the interval between adjacent graduations to represent 10 ft. In this case, the numerals on the scale, instead of representing 10, 20, and so on, will represent 100, 200, and so on. To measure off 360 ft to scale, you should measure from 0 to the 6th graduation beyond the numeral 3. For 800 ft you should measure from 0 to the numeral 8. Because you allowed the interval between adjacent graduations to represent 10 ft, and because the 10 scale has 10 graduations to the in., the scale of your drawing would be 1 in. = 100 ft, or 1/1,200.

Figure 2-26.-Flat metric scale. Metric Scale

The METRIC SCALE is used in the place of the architects and the engineers scale when measurements and dimensions are in meters and centimeters. Metric scales are available in flat and triangular shapes. The flat 30-cm metric scale is shown in figure 2-26. The top scale is calibrated in millimeters and the bottom scale in half millimeters. The triangular metric scale has six fully divided scales, which are 1:20, 1:33 1/3, 1:40, 1:50, 1:80, and 1:100.

When you are using scales on a drawing, do not confuse the engineers scale with the metric scale. They are very similar in appearance. Whenever conversions are made between the metric and English system, remember that 2.54 cm equals 1 in.