A1. An inductor opposes a change in current.
A2. Current lags voltage by 90 (ELI).
A3. Inductive reactance.
A4. X_L = 2pfL.
A5. X_L increases.
A6. X_L decreases.
A7. The capacitor opposes any change in voltage.
A8. Current leads voltage by 90 (ICE).
A9. Capacitive reactance.
A10.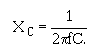
A11. X_C increases.
A12. X_C decreases.
A13. X = X_L - X_C or X = X_C - X_L
A14. 30W (capacitive).
A15. Impedance.
A16.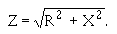
A17. Z = 5W.
A18.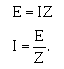

A19. True power is the power dissipated in the resistance of the circuit or the power actually used in the circuit.
A20. Watt.
A21. True Power = (I_R)²R.
A22. Reactive power is the power returned to the source by the reactive components of the circuit.
A23. var.
A24.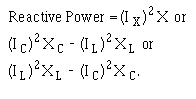
A25. The power that appears to the source because of circuit impedance, or the combination of true power and reactive power.
A26. VA (volt-amperes).
A27.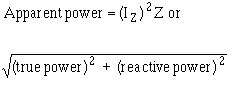
A28. PF is a number representing the portion of apparent power actually dissipated in a circuit.
A29.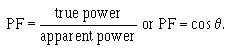
A30. Add 10 ohms of capacitive reactance to the circuit.
A31. In a series circuit impedance is calculated from the values of resistance and reactance. In a parallel circuit, the values of resistive current and reactive current must be used to calculate total current (impedance current) and this value must be divided into the source voltage to calculate the impedance.