POWER RATING

Electrical components are often given a power rating. The power rating, in watts, indicates the rate at which the device converts electrical energy into another form of energy, such as light, heat, or motion. An example of such a rating is noted when comparing a 150-watt lamp to a 100-watt lamp. The higher wattage rating of the 150-watt lamp indicates it is capable of converting more electrical energy into light energy than the lamp of the lower rating. Other common examples of devices with power ratings are soldering irons and small electric motors.

In some electrical devices the wattage rating indicates the maximum power the device is designed to use rather than the normal operating power. A 150-watt lamp, for example, uses 150 watts when operated at the specified voltage printed on the bulb. In contrast, a device such as a resistor is not normally given a voltage or a current rating. A resistor is given a power rating in watts and can be operated at any combination of voltage and current as long as the power rating is not exceeded. In most circuits, the actual power used by a resistor is considerably less than the power rating of the resistor because a 50% safety factor is used. For example, if a resistor normally used 2 watts of power, a resistor with a power rating of 3 watts would be used.

Resistors of the same resistance value are available in different wattage values. Carbon resistors, for example, are commonly made in wattage ratings of 1/8, 1/4, 1/2, 1, and 2 watts. The larger the physical size of a carbon resistor the higher the wattage rating. This is true because a larger surface area of material radiates a greater amount of heat more easily.

When resistors with wattage ratings greater than 5 watts are needed, wirewound resistors are used. Wirewound resistors are made in values between 5 and 200 watts. Special types of wirewound resistors are used for power in excess of 200 watts.

As with other electrical quantities, prefixes may be attached to the word watt when expressing very large or very small amounts of power. Some of the more common of these are the kilowatt (1,000 watts), the megawatt (1,000,000 watts), and the milliwatt (1/1,000 of a watt).

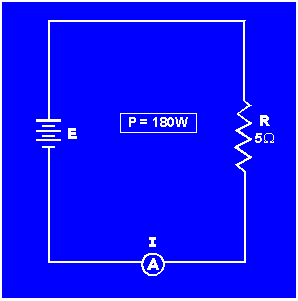
What is the current in a circuit with 5 ohms of resistance that uses 180 watts of power? (refer to figure 3-12)

What type of resistor should be used in the circuit described in question 12?

What is the power used in a circuit that has 10 amperes of current through a 10-ohm resistor?

Figure 3-12. - Circuit for computing electrical quantities.