|
Rules for Series DC Circuits
The same current flows through each part of a series circuit.
The total resistance of a series circuit is equal to the sum of the individual resistances.
The total voltage across a series circuit is equal to the sum of the individual voltage drops.
The voltage drop across a resistor in a series circuit is proportional to the ohmic value of the resistor.
The total power in a series circuit is equal to the sum of the individual powers used by each circuit component.
SERIES CIRCUIT ANALYSIS
To establish a procedure for solving series circuits, the following sample problems will be solved.
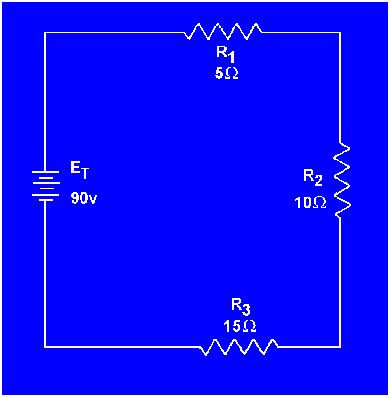
Example: Three resistors of 5 ohms, 10 ohms, and 15 ohms are connected in series with a power source of 90 volts as shown in figure 3-20. Find the total resistance, circuit current, voltage drop of each resistor, power of each resistor, and total power of the circuit.
Figure 3-20. - Solving for various values in a series circuit.
In solving the circuit the total resistance will be found first. Next, the circuit current will be calculated. Once the current is known, the voltage drops and power dissipations can be calculated.
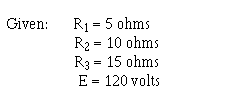
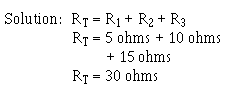
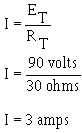
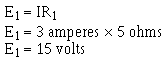
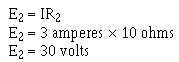
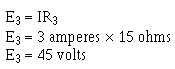
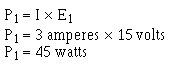
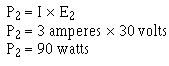
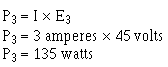
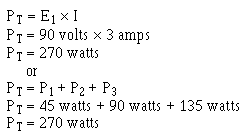
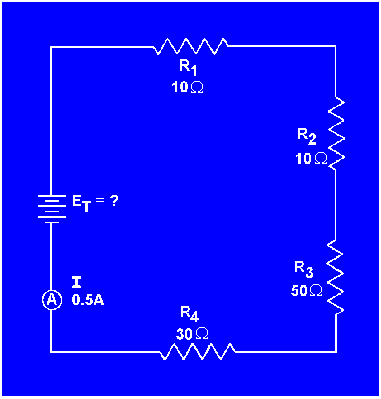
Example: Four resistors, R1 = 10 ohms, R2 = 10 ohms, R3 = 50 ohms, and R4 = 30 ohms, are connected in series with a power source as shown in figure 3-21. The current through the circuit is 1/2 ampere.
What is the battery voltage?
What is the voltage across each resistor?
What is the power expended in each resistor?
What is the total power?
Figure 3-21. - Computing series circuit values.
Given:
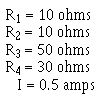
Solution (a):

Solution (b):
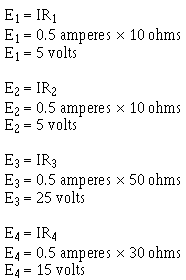
Solution (c):
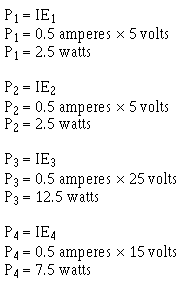
Solution (d):
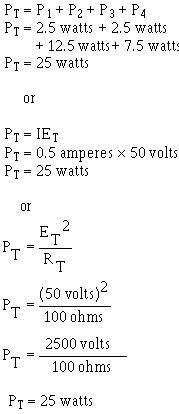
An important fact to keep in mind when applying Ohm's law to a series circuit is to consider whether the values used are component values or total values. When the information available enables the use of Ohm's law to find total resistance, total voltage, and total current, total values must be inserted into the formula. To find total resistance:
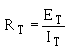
To find total voltage:
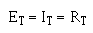
To find total current:
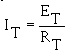
NOTE: IT is equal to I in a series circuit. However, the distinction between IT and I in the formula should be noted. The reason for this is that future circuits may have several currents, and it will be necessary to differentiate between IT and other currents.
To compute any quantity (E, I, R, or P) associated with a single given resistor, the values used in the formula must be obtained from that particular resistor. For example, to find the value of an unknown resistance, the voltage across and the current through that particular resistor must be used.
To find the value of a resistor:
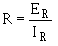
To find the voltage drop across a resistor:
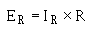
To find current through a resistor:
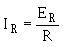
A series circuit consists of two resistors in series. R1 = 25 ohms and R2 = 30 ohms. The circuit current is 6 amps. What is the (a) source voltage, (b) voltage dropped by each resistor, (c) total power, and (d) power used by each resistor?
|
|



