PRACTICE PROBLEMS:

Find the equation of the ellipse with its center at the origin and for which the following properties are given:

ANSWERS:

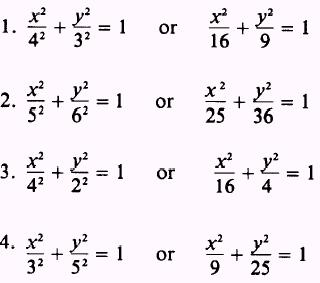
An ellipse may be defined as the locus of all points in a plane, the sum of whose distances from two fixed points, called the foci, is a constant equal to 2a. This is shown as follows:

Let the foci be F, and F_Z at ( c,0), as shown in figure 2-15. Using the standard form of an ellipse,

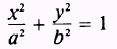
or

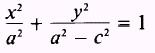
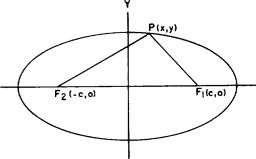
Figure 2-15.-Ellipse, center at origin.

solve for y²:

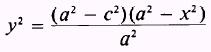
Referring to figure 2-15, we see that

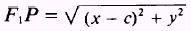
and

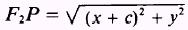
Substitute y² into both equations above and simplify

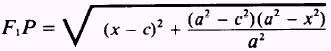
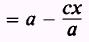
and

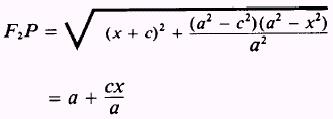
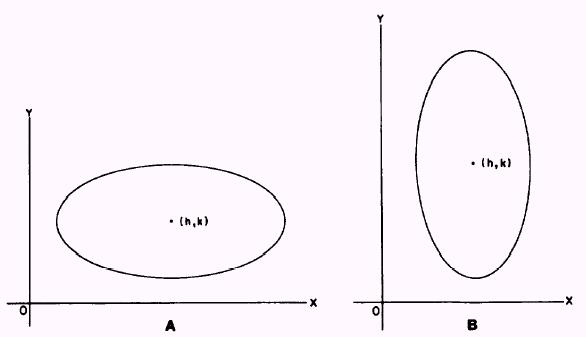
Figure 2-16.-Ellipse, center at (h,k).

so

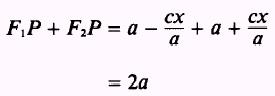
Whenever the center of the ellipse is at some point other than (0,0), such as the point (h,k) in figure 2-16, views A and B, the equation of the ellipse must be modified to the following standard forms:

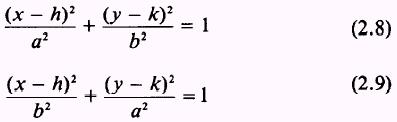
Subtracting h from the value of x reduces the value of the term (x - h) to the value x would have if the center were at the origin. The term (y - k) is identical in value to the value of y if the center were at the origin.

Whenever we have an equation in the general form, such as

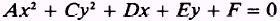
where the capital letters refer to independent constants and A and C have the same sign, we can reduce the equation to the standard form for an ellipse. Completing the square in both x and y and performing a few simple algebraic transformations will change the form to that of equations (2.8) and (2.9).

Theorem: An equation of the second degree, in which the xy term does not exist and the coefficients of x² and y2 are different but have the same sign, represents an ellipse with axes parallel to the coordinate axes.

EXAMPLE: Reduce the equation

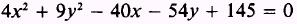
to an ellipse in standard form.

SOLUTION: Collect terms in x and y and remove the common factors of these terms:

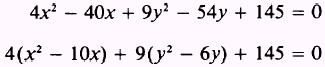
Transpose the constant terms and complete the square in both x and y. When factored terms are involved in completing the square, as in this example, an error is frequently made. The factored value operates on the term added inside the parentheses as well as the original terms. Therefore, the values added to the right side of the equation are the products of the factored values and the terms added to complete the square:

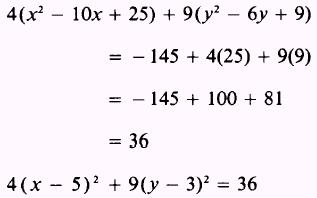
Divide both sides by the right-hand (constant) term. This reduces the right member to 1 as required by the standard form:

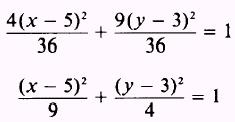
This reduces to the standard form

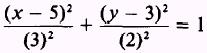
corresponding to equation (2.8). This equation represents an ellipse with the center at (5,3); its semimajor axis, a, equal to 3; and its semiminor axis, b, equal to 2.

EXAMPLE: Reduce the equation

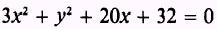
to an ellipse in standard form.

SOLUTION: First, collect terms in x and y. As in the previous example, the coefficients of x² and y2 must be reduced to 1 to complete the square in both x and y. Thus the coefficient of the x² term is divided out of the two terms containing x, as follows:

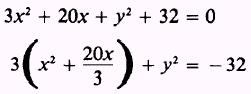
Complete the square in x, noting that a product is added to the

right side:

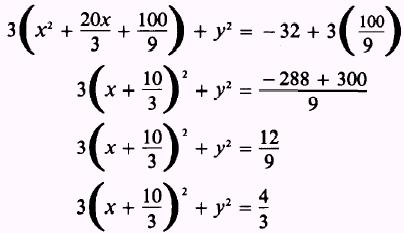
Divide both sides by the right-hand term:

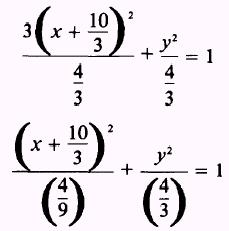
This equation reduces to the standard form,

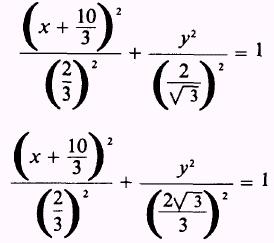
corresponding to equation (2.9), and represents an ellipse with the center at .
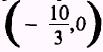