PRACTICE PROBLEMS:

Give the equation; the length of a; and the length of the focal chord for the parabola, which is the locus of all points equidistant from the point and the line, given in the following problems:

ANSWERS:

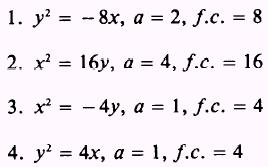
Up to now, all of the parabolas we have dealt with have had a vertex at the origin and a corresponding equation in one of the four following forms:

1. y2 = 4ax

2. y² = - 4ax

3. x2 = 4ay

4. x2 = - 4ay

We will now present four more forms of the equation of a parabola. Each one is a standardized parabola with its vertex at point V(h,k). When the vertex is moved from the origin to the point V(h,k), the x and y terms of the equation are replaced by (x - h) and (y - k). Then the standard equation for the parabola that opens to the right (fig. 2-9, view A) is

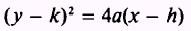
The four standard forms of the equations for parabolas with vertices at the point V(h,k) are as follows:

The method for reducing an equation to one of these standard forms is similar to the method used for reducing the equation of a circle.

EXAMPLE: Reduce the equation

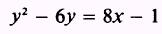
to standard form.

SOLUTION: Rearrange the equation so that the second-degree term and any first-degree terms of the same unknown are on the left side. Then group the unknown term appearing only in the first degree and all constants on the right:

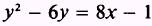
Then complete the square in y:

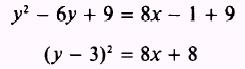
To get the equation in the form

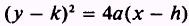
factor an 8 out of the right side. Thus,

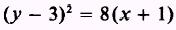
is the equation of the parabola with its vertex at (-1,3).

PRACTICE PROBLEMS:

Reduce the equations given in the following problems to standard form:

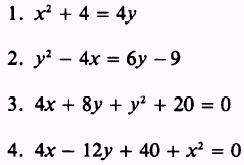
ANSWERS:
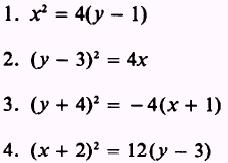