|
EQUAL OR DOUBLE ROOTS
If the discriminant b2 - 4ac equals zero, the
radical in the quadratic formula becomes zero.
In this case the roots are equal; such roots are
sometimes called double roots.
Consider the equation
9x2 + 12x + 4 = 0
Comparing with the general quadratic, we notice that
a = 9, b = 12, and c = 4
The discriminant is

Therefore, the roots are equal.
CHECK: From the formula

The equality of the roots is thus verified.
The roots can be equal only if the trinomial
is a. perfect square. Its factors are equal.
Factoring the trinomial in
9x2 + 12x + 4 = 0
we see that
(3x + 2)2 = 0
Since the factor 3x + 2 is squared, we actually have
3x + 2 = 0
twice, and we have

twice.
The fact that the same root must be counted
twice explains the use of the term "double
root." A double root of a quadratic equation is
always rational because a double root can occur only when the radical vanishes.
REAL AND UNEQUAL ROOTS When the discriminant is positive, the roots
must be real. Also they must be unequal since
equal roots occur only when the discriminant
is zero.
Rational Roots .
If the discriminant is a perfect square, the
roots are rational. For example, consider the
equation
3x2 - x - 2 = 0
in which
a = 3, b = -1, and c = -2
The discriminant is

We see that the discriminant, 25, is a perfect square. The perfect square indicates that
the radical in the quadratic formula can be removed, that the roots of the equation are rational, and that the trinomial can be factored.
In other words, when we evaluate the discriminant and find it to be a perfect square, we know
that the trinomial can be factored.
Thus,

from which
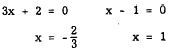
We see that the information derived from the
discriminant is correct. The roots are real,
unequal, and rational.
|

