PROOF:

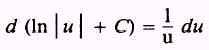
Therefore,

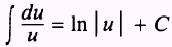
NOTE: The derivative formula 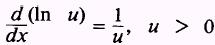, presented in chapter 5, can be extended for negative functions also. Hence,

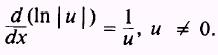
EXAMPLE: Evaluate the integral

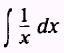
SOLUTION: If we write

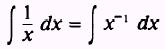
we find we are unable to evaluate

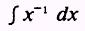
by use of the power of a variable rule, so we write

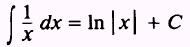
because the 1 dx in the numerator is precisely du and we have fulfilled the requirements for

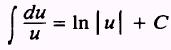
EXAMPLE: Evaluate

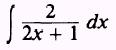
SOLUTION: Let

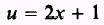
so that

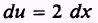
We have the form

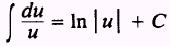
therefore,

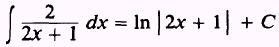
EXAMPLE: Evaluate

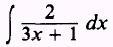
SOLUTION: Let

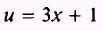
so that

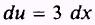
We find we need 3 dx but we have 2 dx. We compensate as follows:

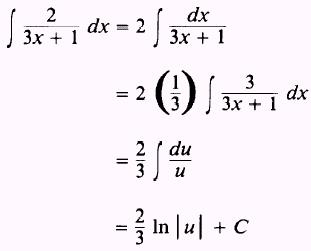
Therefore,
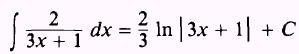