TRIGONOMETRIC FUNCTIONS If we are given

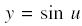
we may state that, from the general formula,

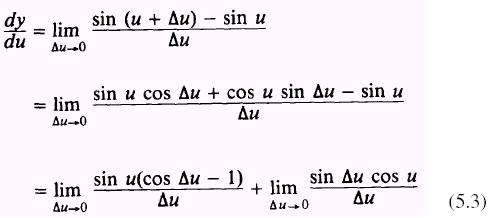
Since

and

Then by substituting equations (5.4) and (5.5) into equation (5.3),

Now we are interested in finding the derivativ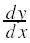e of the function sin u, so we apply the chain rule

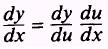
From the chain rule and equation (5.6), we find

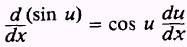
In other words, to find the derivative of the sine of a function, we use the cosine of the function times the derivative of the function.

By a similar process we find the derivative of the cosine function to be

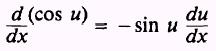
The derivatives of the other trigonometric functions may be found by expressing them in terms of the sine and cosine. That is,

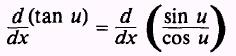
and by substituting sin u for u, cos u for v, and du for dx in the expression of the quotient theorem

we have

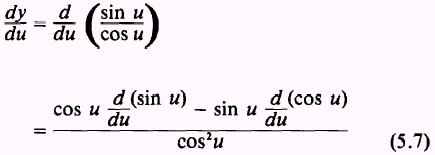
Taking

and

and substituting into equation (5.7), we find that

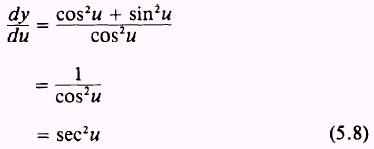
Now using the chain rule and equation (5.8), we find

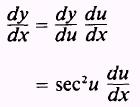
By stating the other trigonometric functions in terms of the sine and cosine and using similar processes, we may find the following derivatives:

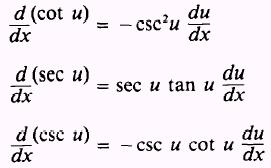
EXAMPLE: Find the derivative of the function

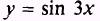
SOLUTION.

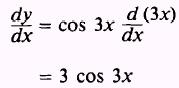
EXAMPLE. Find the derivative of the function

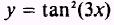
SOLUTION: Use the power theorem to find

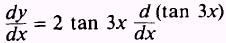
Then find

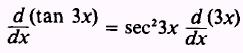
and

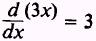
Combining all of these, we find that

PRACTICE PROBLEMS:

Find the derivative of the following:

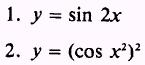
ANSWERS:
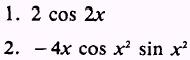