PARAMETRIC EQUATIONS

If the variables x and y of the Cartesian coordinate system are expressed in terms of a third variable, say t (or 9), then the variable

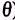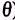t (or ) is called a parameter. The two equations x = x(t) and y = y(t) [or x = x( ) and y = y( 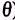)] are called parametric equations.

MOTION IN A STRAIGHT LINE

To illustrate the application of a parameter, we will assume that an aircraft takes off from azoo

field, which we will call the origin. Figure 3-6 shows the diagram we will use. The aircraft is flying on a compass heading of due north. There is a wind blowing from the west at 20 miles per hour, and the airspeed of the aircraft is 400 miles per hour. Let the direction of the positive Y axis be due north and the positive X axis be due east, as shown in figure 3-6. Use the scales as shown.

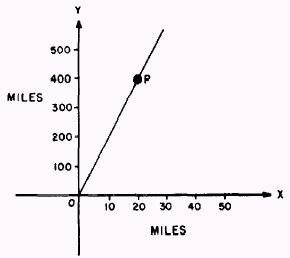
Figure 3-6.-Aircraft position.

One hour after takeoff the position of the aircraft, represented by point P, is 400 miles north and 20 miles east of the origin. If we use t as the parameter, then at any time, t, the aircraft's posi­tion (x,y) will be given by x equals 20t and y equals 400t. The equa­tions are

x = 20t

and

y = 400t

and are called parametric equations. Notice that time is not plotted on the graph of figure 3-6. The parameter t is used only to plot the position (x,y) of the aircraft.

We may eliminate the parameter t to obtain a direct relation­ship between x and y as follows:

if

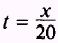
then

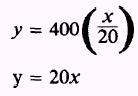
and we find the graph to be a straight line. When we eliminated the parameter, the result was the rectangular coordinate equation of the line.

This information is now available on CD in Adobe PDF Printable Format