The operation of raising a number to a power is a special case of multiplication in which the factors are all equal. In examples such as 4²=4x 4 = 16 and 5³= 5x5x5 =125, the number 16 is the second power of 4 and the number 125 is the third power of 5. The expression 5³ means that three 5s are to be multiplied together. Similarly, 4² means 4 x 4. The first power of any number is the number itself. The power is the number of times the number itself is to be taken as a factor.

The process of finding a root is the inverse of raising a number to a power. A root is a special factor of a number, such as 4 in the expression 4² = 16. When a number is taken as a factor two times, as in the expression 4 x 4 = 16, it is called a square root. Thus, 4 is a square root of 16. By the same reasoning, 2 is a cube root of 8. since 2 x 2 x 2 is equal to 8. This relationship is usually written as 2³ = 8.

A power of a number is indicated by an EXPONENT, which is a number in small print placed to the right and toward the top of the number. Thus, in 4³ = 64, the number 3 is the EXPONENT of the number 4. The exponent 3 indicates that the number 4, called the BASE, is to be raised to its third power. The expression is read "4 to the third power (or 4 cubed) equals 64 ." Similarly, 5²= 25 is read "5 to the second power (or 5 squared) equals 25." Higher powers are read according to the degree indicated; for example, "fourth power," "fifth power," etc.

When an exponent occurs, it must always be written unless its value is 1. The exponent 1 usually is not written, but is understood. For example, the number 5 is actually 5¹ . When we work with exponents, it is important to remember that any number that has no written exponent really has an exponent equal to 1.

A root of a number can be indicated by placing a radical sign, , over the number and showing the root by placing a small number within the notch of the radical sign. Thus, indicates the cube root of 64, and indicates the fifth root of 32. The number that indicates the root is called the INDEX of the root. In the case of the square root, the index, 2, usually is not shown. When a radical has no index, the square root is understood to be the one desired. For example, indicates the square root of 36. The line above the number whose root is to be found is a symbol of grouping called the vinculum. When the radical symbol is used, a vinculum, long enough to extend over the entire expression whose root is to be found, should be attached.

Practice problems. Raise to the indicated power or find the root indicated.

Raising to a power is multiplication in which all the numbers being multiplied together are equal. The sign of the product is determined, as in ordinary multiplication, by the number of minus signs. The number of minus signs is odd or even, depending on whether the exponent of the base is odd or even. For example, in the problem

2³ = (-2)(-2)(-2) = -8

there are three minus signs. The result is negative. In

Positive and negative numbers belong to the class called REAL NUMBERS. The square of a real number is positive. For example, (-7)² = 49 and 7² = 49. The expression (-7)² is read "minus seven squared." Note that either seven squared or minus seven squared gives us +49. We cannot obtain -49 or any other negative number by squaring any real number, positive or negative.

Since there is no real number whose square is a negative number, it is sometimes said that the square root of a negative number does not exist. However, an expression under a square root sign may take on negative values. While the square root of a negative number cannot actually be found, it can be indicated.

The indicated square root of a negative number is called an IMAGINARY NUMBER. The number , for example, is said to be imaginary. It is read "square root of minus seven." Imaginary numbers are discussed in chapter 15 of this course.

We recall that the exponent of a number tells the number of times that the number is to be taken as a factor. A fraction is raised to a power by raising the numerator and the denominator separately to the power indicated. The expression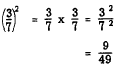 means 3/7 is used twice as a factor. Thus,

Since a minus sign can occupy any one of three locations in a fraction, notice that evaluating (-1/5)² is equivalent to

The process of taking a root of a number is the inverse of the process of raising the number to a power, and the method of taking the root of a fraction is similar. We may simply take the root of each term separately and write the result as a fraction. Consider the following examples:

1. 1/9 
2. 9/16
3. 36/25
4. 8/27
5. 4/6 
6. 4/5
7. 2/3 
8. 3/7