|
OBLIQUE TRIANGLES
Oblique triangles were defined in chapter 17 of
this training course as triangles which contain no right angles. A natural
approach to the solution of problems
involving oblique triangles is to construct
perpendicular lines and form
right triangles which subdivide the original
triangle. Then the problem is solved by the usual methods
for right triangles.
DIVISION. INTO RIGHT .TRIANGLES
The oblique triangle ABC in figure 19-18 has
been divided into two right triangles by drawing
line BD perpendicular to AC. The length of AC
is found as follows:
1. Find the length of AD.

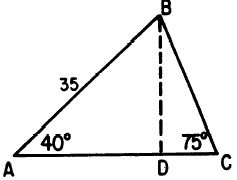
Figure 19-18.-Finding the unknown parts of
an oblique triangle.
CAUTION: A careless appraisal of this problem may lead the unwary trainee to
represent
the ratio AC/AB as the cosine of
40. This error is avoided only by the
realization that the trigonometric ratios are
based on RIGHT triangles.
2. In order to find the length of DC, first calculate
BD.

3. Find the length of DC
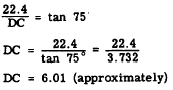
4. Add AD and DC to find AC.
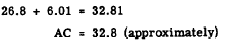
SOLUTION BY SIMULTANEOUS EQUATIONS
A typical problem in trigonometry is the determination
of the height of a point such as B in figure
19-19.
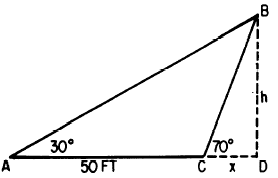
Figure 19-19.-Calculation of unknown quantities
by means of oblique triangles.
Suppose that point B is the top of a hill, and point
D is inaccessible. Then the only measurements possible on the ground are those
shown in figure 19-19. If we let h represent BD
and x represent CD, we can set up the following system of simultaneous
equations:
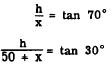
Solving these two equations for h in terms of x,
we have
h= x tan 70
and
h = (50 + x) tan 30
Since the two quantities which are both equal to
h must be equal to each other, we have

Knowing the value of x, it is now possible to compute
h as follows:

Practice problems:
1. Find the length of side BC in figure 19-20 (A).
2. Find the height of point B above line AD in
figure
19-20 (B).
Answers:
1. 21.3 feet
2. 41.7 feet
|

