Practice Circuit Problem
Figure 3-55 is a typical combination circuit. To make sure you understand the techniques of solving for the unknown quantities, solve for E_R1.

Figure 3-55. - Combination practice circuit.

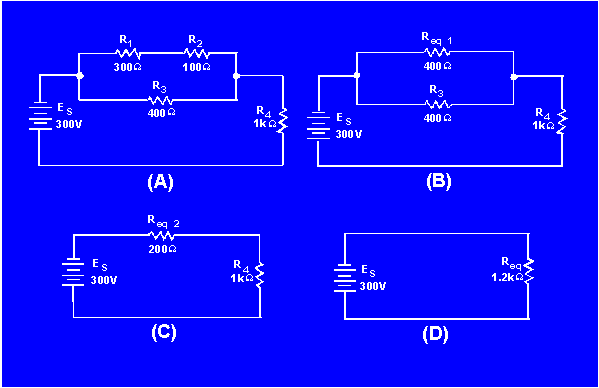
It is not necessary to solve for all the values in the circuit to compute the voltage drop across resistor R₁ (E _R1). First look at the circuit and determine that the values given do not provide enough information to solve for E_R1 directly.

If the current through R₁ (I_R1) is known, then E_R1 can be computed by applying the formula:


The following steps will be used to solve the problem.

>The total resistance (R_T) is calculated by the use of equivalent resistance.

Given:


Solution:


Redraw the circuit as shown in figure 3-55(B).

Given:


Solution:


Solution:


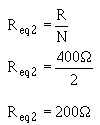
Redraw the circuit as shown in figure 3-55(C).

Given:


Solution:


The total current (I_T) is now computed.

Given:


Solution:


>Solve for the voltage dropped across R_eq2. This represents the voltage dropped across the network R₁, R₂, and R₃ in the original circuit.

Given:


Solution:


>Solve for the current through R_eq1. (R_eq1 represents the network R₁ and R₂ in the original circuit.) Since the voltage across each branch of a parallel circuit is equal to the voltage across the equivalent resistor representing the circuit:

Given:


Solution:


Solve for the voltage dropped across R₁ (the quantity you were asked to find). Since R_eq1 represents the series network of R₁ and R₂ and total current flows through each resistor in a series circuit, I_R1 must equal I_Req1.

Given:


Solution:


Refer to figure 3-55(A). If the following resistors were replaced with the values indicated: R₁ = 900Ω, R₃ = lkΩ, what is the total power in the circuit? What is E_R2?