SOLUTION: Substituting into equation (6.7), we have

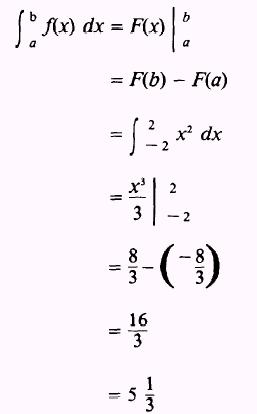
The area above a curve and below the X axis, as shown in figure 6-11, will, through integration, furnish a negatvie answer.

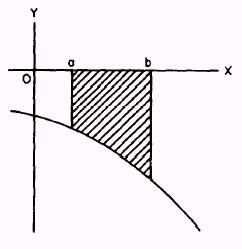
Figure 6-11.-Area above a curve.

If the graph of y = f(x), between x = a and x = b, has portions above and portions below the X axis, as shown in figure 6-12, then

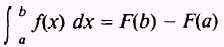
is the sum of the absolute values of the positive areas above the X axis and the negative areas below the X axis, such that

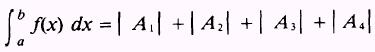
where

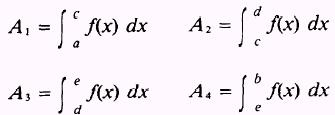
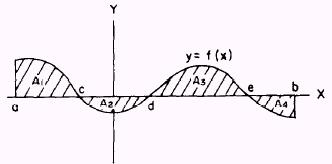
Figure 6-12.-Areas above and below a curve.

EXAMPLE: Find the areas between the curve

y=x

and the X axis bounded by the lines

x= -2

and

x=2

as shown in figure 6-13.

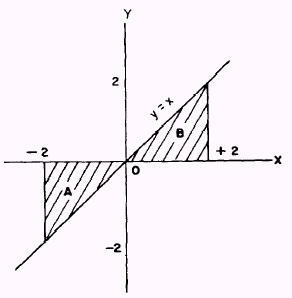
Figure 6-13.-Negative and positive value areas.

SOLUTION. These areas must therefore, we write be computed separately;

and the absolute value of - 2 is

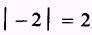
Then,

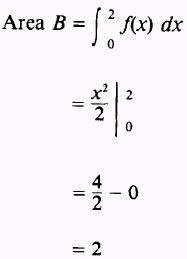
Adding the two areas, , we find

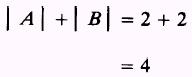
NOTE: If the function is integrated from - 2 to 2, the following INCORRECT result will occur:

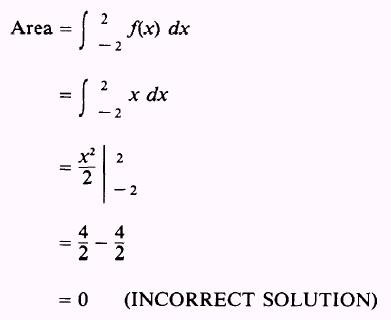
This is obviously not the area shown in figure 6-13. Such an example emphasizes the value of making a commonsense check on every solution. A sketch of the function will aid this commonsense judgement.

EXAMPLE: Find the total area bounded by the curve

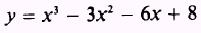
the X axis, and the lines

x= -2

and

x=4

as shown in figure 6-14.

SOLUTION. The area desired is both above and below the X axis; therefore, we need to find the areas separately and then add them together using their absolute values.

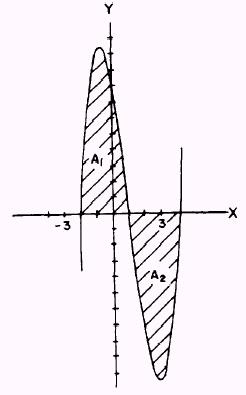
Figure 6-14.-Positive and negative value areas.

Therefore,

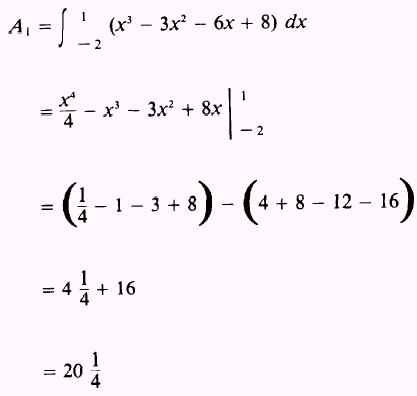
and

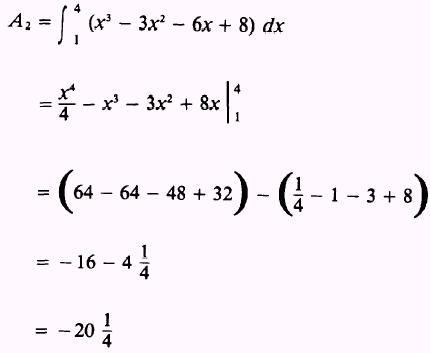
Then, the total area is
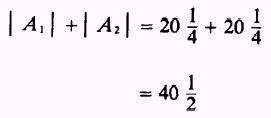