Since a given number can be located in three positions on the K scale, the question arises as to which third of the K scale to use when locating a number. Generally, the left index, the left middle index, the right middle index, and the right index are considered to be numbered as shown in figure 8-7.

Figure 8-7.-Powers of 10 associated with K-scale indices.

A system similar to that used with square roots may be used to locate the position of a number on the K scale. Groups of three are used rather than groups of two. The grouping for cube root is illustrated as follows:

For whole or mixed numbers the following rules apply:

1. If the left-hand group contains one digit, locate the number in the left third of the K scale.

2. If the left group contains two digits, locate the number in the middle third of the K scale.

3. If the left group contains three digits, locate the number in the right third of the K scale.

The following examples illustrate the foregoing rules:

1.
(One digit)-left third K scale.

3.
(Three digits)-right third of K scale. 

For positive numbers less than one, look from left to right and find the first group that contains a digit other than zero.

1. If the first two figures in this group are zeros, locate the number in the left third of the K scale.

2. If only the first figure in this group is zero, locate the number in the middle third of the K scale.

3. If the first figure of the group is not zero, locate the number in the right third of the K scale.

The following examples illustrate these rules:

2.
(One zero)-middle third K scale.

PLACING THE DECIMAL POINT.-To place the decimal point in the cube root of a number, we use the system of marking off in groups of three as shown above.

For whole or mixed numbers, there is one digit in the root to the left of the decimal point for every group marked in the original number. Thus,

For positive numbers less than one, there will be one zero in the root between the decimal point and the first significant digit for every three zeros counted between the decimal point and the first significant digit of the original number. Thus,

(Two zeros between decimal point and first significant digit of root.)

Place the hairline over 216 in the right third of the K scale. Read the digit sequence, 6, under the hairline on the D scale. Since there are two groups in the original number, there are two digits to the left of the decimal point in the root. Thus,

EXAMPLE: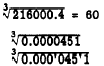
(Only first figure is zero in this group)

Place the hairline over 451 in the middle third of the K scale. Read the digit sequence, 357, under the hairline on the D scale. Since there is one group of three zeros, there is one zero between the decimal point and the first significant digit of the root. Thus,

POWERS OF 10.-To take the cube root of a power of 10, mark it off as explained in the preceding paragraphs. The number in the left group will then be 1, 10, or 100. We know that the cube root of 10 is a number between 2 and 3. Thus, for the cube root of any number whose left group is 10, use the K scale index which lies between 2 and 3 on the D scale. The cube root of 100 lies between 4 and 5. Therefore, for a number whose left group is 100, use the K scale index between 4 and 5 on the D scale. 

Practice problems. Following are some problems and the digit sequence (d. 6.) of the roots. Locate the decimal point for each root.

Answers: