To explain the cases that arise in problems involving percents, it is necessary to define the terms that will be used. Rate (r) is the number of hundredths parts taken. This is the number followed by the percent sign. The base (b) is the whole on which the rate operates. Percentage (p) is the part of the base determined by the rate. In the example

5% is the rate, 40 is the base, and 2 is the percentage.

There are three cases that usually arise in dealing with percentage, as follows:

Case I-To find the percentage when the base and rate are known.

Case II-To find the rate when the base and percentage are known.

EXAMPLE: The number 5 is 25% of what number ?

Case I
    In the example

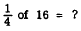
In other words, "of" means to multiply. Thus, to find the percentage, multiply the base by the rate. Of course the rate must be changed from a percent to a decimal before multiplying can be done. Rate times base equals percentage.

FRACTIONAL PERCENTS.-A fractional percent represents a part of 1 percent. In a case such as this, it is sometimes easier to find 1 percent of the number and then find the fractional part. For example, we would find 1/4 percent of 840 as follows:

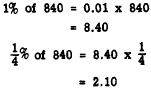
To explain case II and case III, we notice in the foregoing example that the base corresponds to the multiplicand, the rate corresponds to the multiplier, and the percentage corresponds to the product.

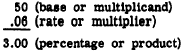
Recalling that the product divided by one of its factors gives the other factor, we can solve the following problem:

We then divide the product (percentage) by the multiplicand (base) to get the other factor (rate). Percentage divided by base equals rate. The rate is found as follows:

The rule for case II, as illustrated in the foregoing problem, is as follows: To find the rate when the percentage and base are known, divide the percentage by the base. Write the quotient in the decimal form first, and finally as a percent.

The unknown factor in case III is the base, and the rate and percentage are known.

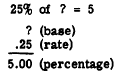
We divide the product by its known factor to find the other factor. Percentage divided by rate equals base. Thus,

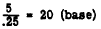
The rule for case III may be stated as follows: To find the boss when the rate and percentage are known, divide the percentage by the rate.

Practice problems. In each of the following problems, fact determine which case is involved; then find the answer.