|
SUBTRACTION
The rule of likeness applies in the subtraction of fractions as well as in
addition. Some examples will show that cases
likely to arise may be solved by use of ideas
previously developed.
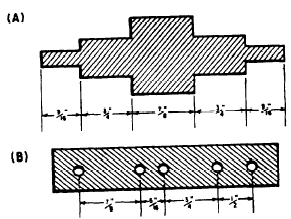
Figure 4-5.-Adding fractions to obtain total
length or spacing.
EXAMPLE: Subtract 1 1/3 from 5 2/3
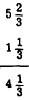
We see that whole numbers are subtracted from whole
numbers; fractions from fractions.
EXAMPLE: Subtract 1/8 from 4/5
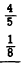
Changing to like
fractions with an LCD, we have
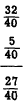
EXAMPLE: Subtract 11/12 from 3 2/3
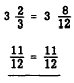
Regrouping 3 8/12 we have
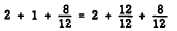
Then
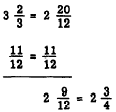
Practice problems. Subtract the lower number from the upper number and reduce
the difference to simplest terms:

The following problem demonstrates subtraction of fractions in a practical
situation.
EXAMPLE: What is the length of the dimension marked X on the machine bolt
shown in figure 4-8 (A)?
SOLUTION: Total the lengths of the known parts.
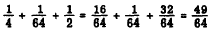
Subtract this sum from the overall length.
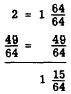
The answer is 1 15/64 inch
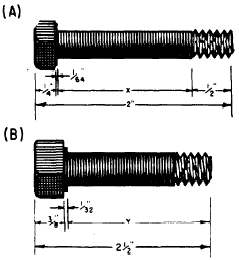
Figure 4-6.-Finding unknown dimensions by
subtracting fractions.
Practice problem. Find the length of the dimension
marked Y on the machine bolt in figure 4-6
(B).
Answer 2 3/32 inches
|

