|
FINDING THE CENTER OF
A CIRCLE
It is sometimes necessary to find the center of
a circle of which only an arc or a segment is given.
(See fig. 18-8.)
From any point on the am, such as A, draw two
chords intersecting the arc in any two Points,
such as B and C. With the points A, B, and C
as centers, use any convenient radius and
draw short intersecting arcs to form the perpendicular
bisectors of chords AC and AB. Join the
intersecting arcs on each side of AC, obtaining
line MP, and join the arcs on each side of
AB, obtaining line NQ. The intersection of MP
and NQ is point 0, the center of the circle.
ELLIPSES
An ellipse of specified length and width is constructed
as follows:
1. Draw the major axis, AB, and the minor axis,
CD, as shown in figure 18-9.
2. On a straightedge or ruler, mark a point (labeled
a in the figure) and from this point measure
one-half the length of the minor axis and
make a second mark (b in figure 18-9). From
point a, measure one-half the length of

Figure 18-6. - Constructing a right angle by the
3-4-5 method.
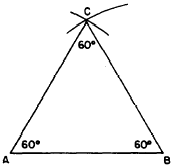
Figure 18-7 - Constructing 60
angles.
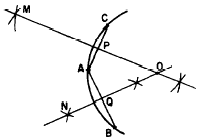
Figure 18-8 - Finding the center of
a circle.
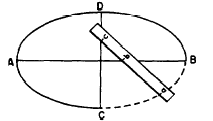
Figure 18-9.-Constructing an ellipse.
the major axis and make a third mark (c in the figure).
3. Place the straightedge on the axes so that b
lies on the major axis and c lies on the minor axis.
Mark the paper with a dot beside point a. Reposition
the straightedge, keeping b on the major axis
and c on the minor axis, and make a dot
beside the new position of a.
4. After locating enough dots to see the elliptical pattern,
join the dots with a smooth curve.
SOLID FIGURES
The plane figures discussed in chapter 17 of this
course are combined to form solid figures. For
example, three rectangles and two triangles may
be combined as shown in figure 18-10. The
flat surfaces of the solid figure are its FACES;
the top and bottom faces are the BASES, and
the faces forming the sides are the LATERAL FACES.
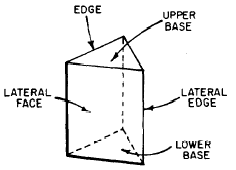
Figure 18-10.-Parts of a solid figure.
Some solid figures do not have any flat faces, and
some have a combination of curved surfaces and
flat surfaces. Examples of solids with curved
surfaces include cylinders, cones, and spheres.
|

