Custom Search
|
|
  |
|
|
Irrational Roots If the discriminant is not a perfect square, the radical cannot be removed and the roots are irrational.Consider the equation 2x2 - 4x + 1 = 0 in which a = 2, b = -4, and c = 1. The discriminant is
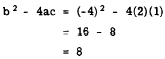
This discriminant is positive and not a perfect square. Thus the roots are real, unequal, and irrational.To check the correctness of this information, we derive the roots by means of the formula. Thus,
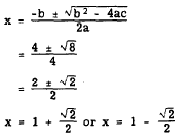
This verifies the conclusions reached in evaluating the discriminant. When the discriminant is a positive number, not a perfect square, it is useless to attempt to factor the trinomial. The formula is needed to find the roots. They will be real, unequal, and irrational.SUMMARY The foregoing information concerning the discriminant may be summed up in the follow- ing four rules: 1. If b2- 4ac is a perfect square or zero, the roots are rational; otherwise they are irrational.2. If b2- 4ac is negative (less than zero), the roots are imaginary.3. If b2 - 4ac is zero, the roots are real, equal, and rational.4. If b2 - 4ac is greater than zero, the roots are real and unequal.Practice problems. Determine the character of the roots of each of the following equations:
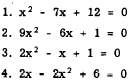
Answers: 1. Real, unequal, rational |
 
|
