|
USING TWO VARIABLES IN
SOLVING WORD PROBLEMS
Many problems can be solved quickly and
easily using one equation with one variable.
Other problems that might be rather difficult to
solve in terms of one variable can easily be
solved using two equations and two variables.
The difference in the two methods is shown in
the following example, solved first by using one
variable and then using two.
EXAMPLE: Find the two numbers such that
half the first equals a third of the second and
twice their sum exceeds three times the second
by 4.
SOLUTION USING ONE VARIABLE:
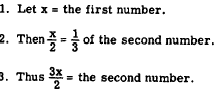
From the statement of the problem, we then have
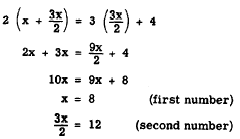
SOLUTION USING TWO VARIABLES:
If we let x and y be the first and second numbers, respectively, we can write two equations
almost directly from the statement of the problem. Thus,
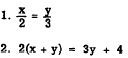
Solving for x in the first equation and substituting this value in the second, we have
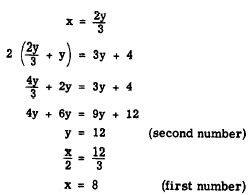
Thus, we see that the solution using two variables is more direct and simple. Often it would
require a great deal of skill to manipulate a
problem so that it might be solved using one
variable; whereas the solution using two variables might be very simple. The use of two
variables, of course, involves the fact that the
student must be able to form two equations
from the information given in the problem.
Practice problems. Solve the following problems using two variables:
1. A Navy tug averages 12 miles per hour downstream and 9 miles per hour upstream. How
fast is the stream flowing?
2. The sum of the ages of two boys is 18. If 4
times the younger boys age is subtracted from
3 times the older boys age, the difference is
12. What are the ages of the two boys?
Answers:
1. 1 1/2 mph.
2. 6 years and 12 years.
INEQUALITIES IN TWO VARIABLES
Inequalities in two variables are of the following form:
x+y>2
Many solutions of such an inequation are apparent immediately. For example, x could have
the value 2 and y could have the value 3, since
2 + 3 is greater than 2.
The existence of a large number of solutions
suggests that a graph of the inequation would
contain many points. The graph of an inequation in two unknowns is, in fact, an entire area
rather than just a line.
|

